速さと速度(3)

距離は速さと同様、大きさのみを表すスカラー量です。ではベクトル量は？というと変位という用語を使います。変位とは位置の変化であり、もともといた位置からのどれほど移動したかを表すベクトル量です。ここでは変位は\(x\)で表します。
ベクトルを表すとき、文字の上に→を書いて\(\overrightarrow{x}\)とします。同じように速度ベクトルも\(\overrightarrow{v}\)とします。
一方で、時間は同じ方向にしか進まなにのでベクトル量ではなくスカラー量です。
さて、このベクトル量で\(\overrightarrow{v}\)を定義してみましょう。
変位ベクトル\(\overrightarrow{x}\)は元の位置からの変化を意味します。そこで、時間\(t_0\)のときの位置を\(\overrightarrow{x_0}\)とし、\(x_0\)から\(t\)秒後の時間\(t_1\)のときの位置を\(\overrightarrow{x_1}\)とします。このときの変位を\(\Delta\overrightarrow{x}=\overrightarrow{x_1}-\overrightarrow{x_0}\)で表します。\(\Delta\)は差を表す記号でデルタと読みます。
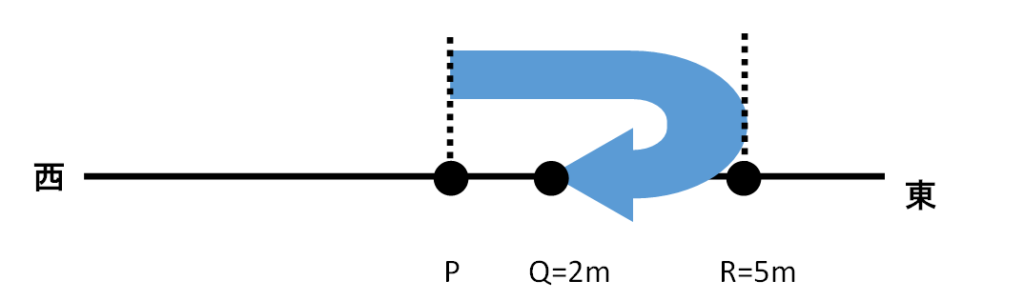
時間も同じように\(\Delta t=t_1-t_0\)として平均の速度\(\overrightarrow{v}\)は \[\large{\overrightarrow{v}=\frac{\Delta\overrightarrow{x}}{\Delta t}=\frac{\overrightarrow{x_1}-\overrightarrow{x_0}}{t_1-t_0}}\] なお、変位は位置の変化であるから、下図のように東へ5mの点Rに進んでから西へ3m戻って点Qに到達したとき、変位は2mということになります。ちなみに距離は7mです。