速さと速度(4)

2023年10月28日 2023年10月28日

Physics

通常、物理で速さや速度というときは平均の速度（速さ）ではなく瞬間の速度（速さ）を対象にします。平均の速度はある時間\(t_0\)から\(t_1\)まで進んだときに対する変位の変化の比なので、 \[\large{\overline{\overrightarrow{v}}=\frac{\Delta x}{\Delta t}=\frac{\overrightarrow{x_1}-\overrightarrow{x_0}}{t_1-t_0}}\] これは2点間の直線の傾きを意味しています。

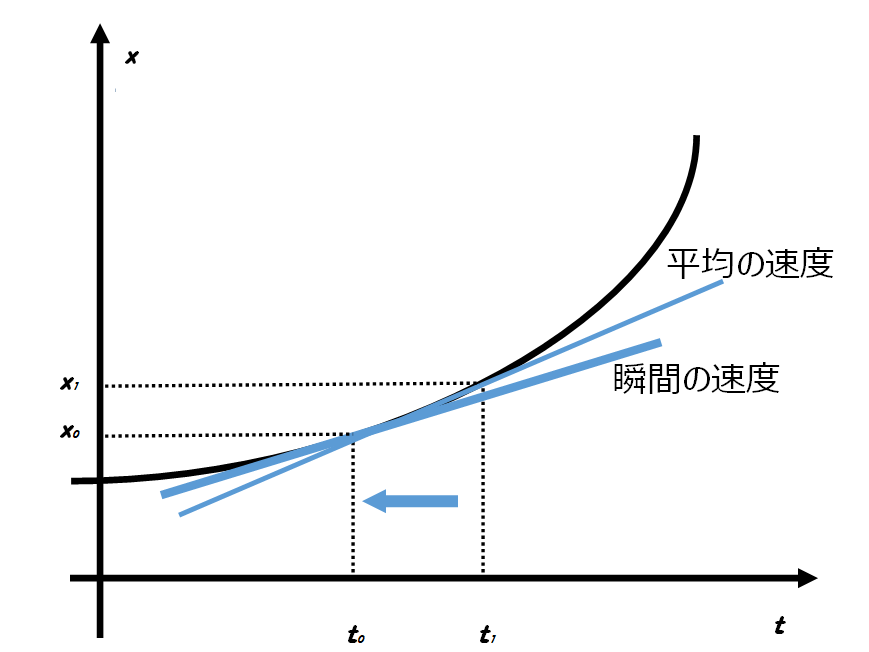
ここで、時間\(\Delta t\)の間隔をどんどん狭めて、つまり\(t_1\)をどんどん\(t_0\)にほぼ重なるくらいに狭めると、そのときの速度は点\((t_0,x_0)\)における接線の傾きに等しくなります。このときの傾きが瞬間の速度を表します。なお、数式では\(\Delta\)から\(d\)（＝さらに微小な範囲）に書き換えて瞬間の速度\(\overrightarrow{v}\)は \[\large{\overrightarrow{v}=\frac{d\overrightarrow{x}}{dt}}\] で表します。

※\(\overline{\overrightarrow{v}}\)の上についている横線は平均を表しバーと読む
※瞬間の速度は微分の定義そのものです

カテゴリー: 力学

速さと速度(4)

コメントを残すコメントをキャンセル

速さと速度(3)

速さと速度(5)

コメントを残す コメントをキャンセル

速さと速度(3)

速さと速度(5)

コメントを残すコメントをキャンセル