速度の合成(1)

速度はベクトル量です。そのため大きさだけでなく向きも重要な要素です。ここからは速度の合成について考えていきます。
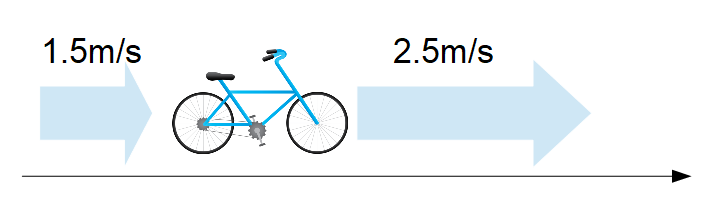
今、下図のように右向きを正として右に向かって風速1.5m/sの追い風の中を自転車がやはり右向きに2.5m/sで進んでいることを想定します。
このとき、地上で静止している人から見た、自転車の速度はどれくらいになるでしょうか？

自転車に乗っている人の感覚として、追い風ならそれほど力を入れて漕がなくても速度は出ている感じがすると思います。これは物理的にも正しいことで、地上で静止している人からすれば、追い風と自転車の速度を足した速度 \[\large{1.5\text{[m/s]}+2.5\text{[m/s]}=4.0\text{[m/s]}}\] が自転車の速度として認識されます。
つまり、自転車は右向きに4.0m/sで進んでいるように見えます。

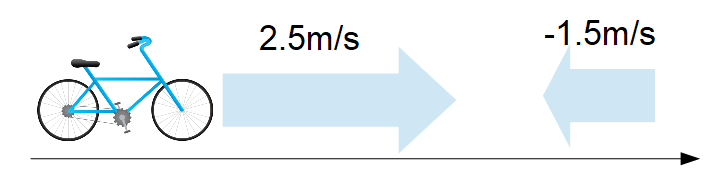
一方、左向きに風速1.5m/sの逆風が吹いていたらどうでしょうか？

右向きを正としていましたから左向きは-1.5m/sとすることができます。地上で静止している人から見れば自転車の速度は同じように足し合わせたものになるから \[\large{-1.5\text{[m/s]}+2.5\text{[m/s]}=1.0\text{[m/s]}}\] となり、右向きに1.0m/sで進んでいるように見えます。
このように2つ以上の速度を足し合わせることを速度の合成といい、足し合わせた速度のことを合成速度といいます。