速度の合成(3)
Physics（１）自転車はA地点からB地点まで何秒かかるか求めよ。
（２）自転車がA地点からB地点到達後、またA地点まで戻ってくるのに何秒かかるか求めよ。
（１）右向きを正として考えると、A地点からB地点までは追い風なので自転車の合成速度は、3.0[m/s]+1.5[m/s]=4.5[m/s]。
よって
\[\large{450\text{[m]}\div 4.5\text{[m/s]}=\underline{100\text{[s]}}}\]
※有効数字は桁の少ないほうに合わせる
（２）B地点からA地点への戻りの自転車の速度はどうなるでしょうか？
自転車は左向きに進むので-3.0[m/s]。一方、風は変わらず右向きに1.5m/sで吹いているので、自転車の合成速度は、-3.0[m/s]+1.5[m/s]=-1.5[m/s]。つまり左向きに1.5m/sで進んでいます。AB間の距離は450mですので、B地点からA地点への戻るときの時間は、450[m]÷1.5[m/s]=300[s]。したがって、行きは100[s]かかっているから
\[\large{100\text{[s]}+300\text{[s]}=\underline{400\text{[s]}}}\]
（１）川の流れが1.0m/sのとき、岸にいる人から見た船の速度を求めよ。ただし、\(\sqrt{2.0}=1.4,\sqrt{3.0}=1.7,\sqrt{5.0}=2.2\)とする。
（２）向こう岸まで着いたときにB地点からどれくらい下流に流されているか求めよ。
（１）状況を模式的に表せば以下のようになります。
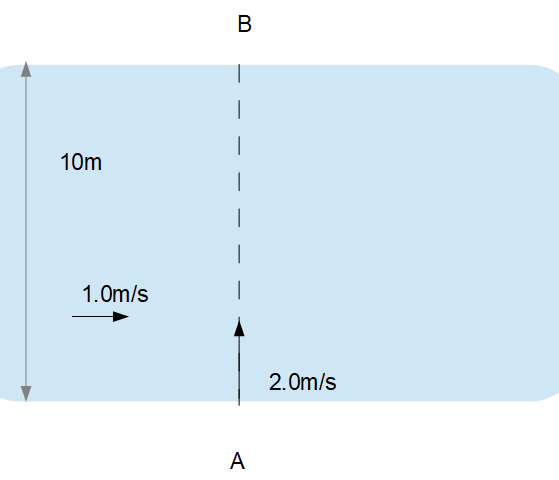
岸にいる人からすれば、川下に流されているように見えるはずです。船の速度は2.0m/s、川の流れは1.0m/sであるから以下のような直角三角形が見え、三平方の定理より斜辺は\(\sqrt{2.0^2+1.0^2}=\sqrt{5.0}=2.2\)。よって、岸にいる人からすれば2.2m/sで進んでいるように見えます。
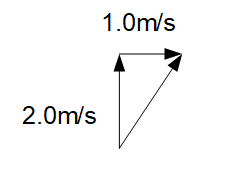
（２）（１）で使った直角三角形を利用し、向こう岸まで10mだから以下のような図を作ります。
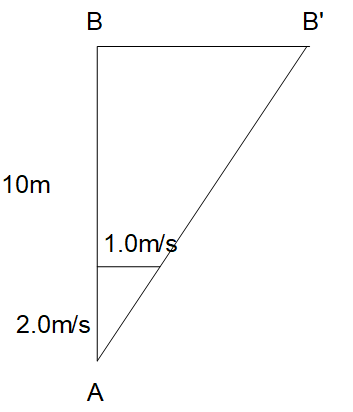1秒間では2.0m船が進むごとに1.0m川下に流されるから、10mでは？というと、\(2.0:1.0=10:x\)より\(x=5.0\)。つまり5.0mだけB地点より下流に流されます。
