相対速度(1)

今までの速度というのは、あくまでも観測者が静止しているというのを前提に考えてきていました。つまりは、自転車が走っていたり、船が進んでいたりというのを観測している人が動いていない状態でどれくらいの速度があるのかということを考えてきたわけです。
ただ、実際はその観測者も動いているというのはよくあることだと思います。実際の例でみてみましょう。

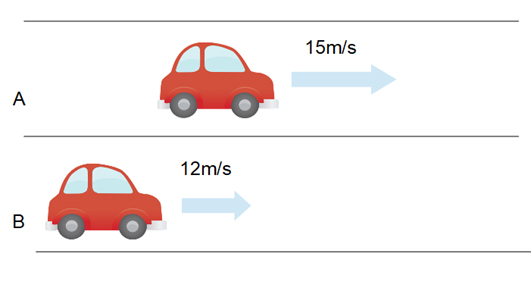
上記のように右向きを正として、15m/sで走る車Aと12m/sで走る車Bがあったとします。このとき、自分が車Bに乗っていたとすると、車Aがどのように見えるかを考えます。当然、自分の車Bよりも車Aの速度が大きいですから車Aはどんどん右向きに遠ざかっていくはずです。

車Bの速度\(v_B=\)12m/s、と車Aの速度\(v_A=\)15m/sでその速度差は15m/s-12m/s=3m/sなので、車Bから見れば車Aは3m/sの速度で走っているように見えます。
この車Bから見た車Aの速度を相対速度といい、「車Bに対する車Aの相対速度」と一般的に言って\(v_{BA}\)と表記します。ただし、この表現はわかりにくいのも事実なので、「車Bから見た車Aの相対速度」と読み替えた方がわかりやすいかもしれません。

逆に、車Aから見た車Bの相対速度はどうなるでしょうか。車Aから見れば車Bの方が速度が遅いので徐々に左向きに遠ざかっていくはずです。左向きは負ですからマイナスの速度を持つはずです。先にみたように車Aと車Bの速度差は3m/sですから車Aから見た車Bの相対速度は-3m/sと計算できます。数式で表すと\(v_{AB}=12\text{[m/s]}-15\text{[m/s]}=-3\text{[m/s]}\)となります。

一般的に、Aに対するBの相対速度は以下のようにあらわされます。