相対速度(2)

相対速度の計算で、常に同じ方向に動いているわけではないので、今度は車Aが左向きに、車Bが右向きに動いている様子で考えてみます。速度は前回の記事と同じもので考えていきましょう。

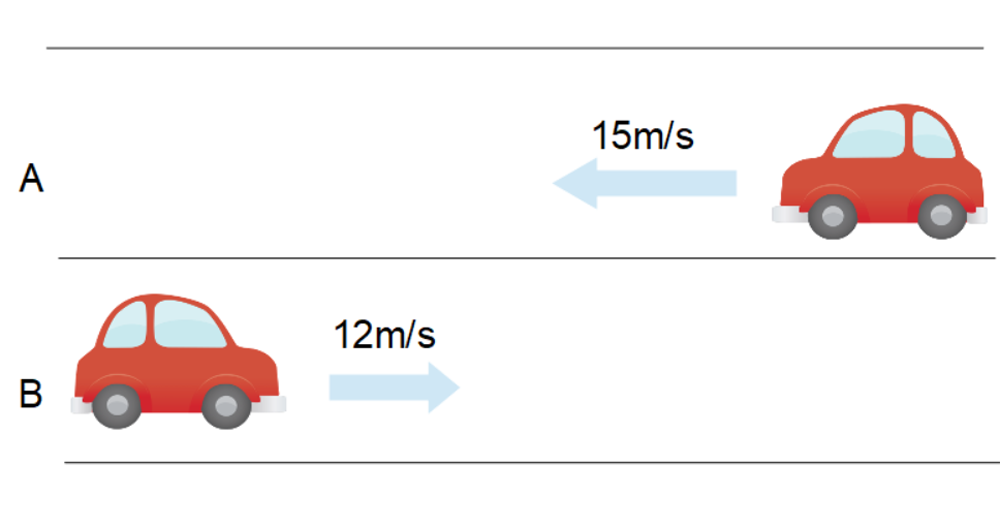
右向きを正とすると、車Aの速度は\(v_{A}=-\)15m/s、車Bの速度は\(v_{B}=\)12m/sとなります。相対速度の考え方は変わらずです。このとき、車Aに対する車Bの相対速度を計算してみましょう。

\[\large{v_{AB}=12\text{[m/s]}-(-15\text{[m/s]})=27\text{[m/s]}}\]

物理は数式を単なる計算としてはみません。数式とその結果がどのような意味を持っているかを考えることが重要です。

上記計算結果は27m/sです。正の値を示していますから、右向きに27m/sという速度で動いているように車Aからは見えるわけです。要するに車Aに乗っている人からすれば、車Bは27m/sの速度で自分に向かってくるということです。道路などですれ違う時に恐怖を感じるのはこのためです。

一方、車Bからみた車Aの相対速度は、 \[\large{v_{BA}=-15\text{[m/s]}-12\text{[m/s]})=-27\text{[m/s]}}\] です。速度の絶対値は同じですが、符号が違って今回は負です。ということは、車Bから見れば車Aは左向きに27m/sの速度で見えるということになります。