加速度(2)
加速度がある状態での\(v-t\)グラフはどのようになるでしょうか。等速直線運動であれば傾きのない直線となります(加速度がゼロ)が、加速度が変化しない物体の運動であれば、一次関数的な直線となります。このとき、\(a>0\)であれば右上がりの直線に、\(a<0\)なら右下がりの直線となります。
加速度が正は徐々に速度が上がっていくということ、一方、加速度が負ということは徐々に速度が遅くなっていくという物体の運動を意味しています。
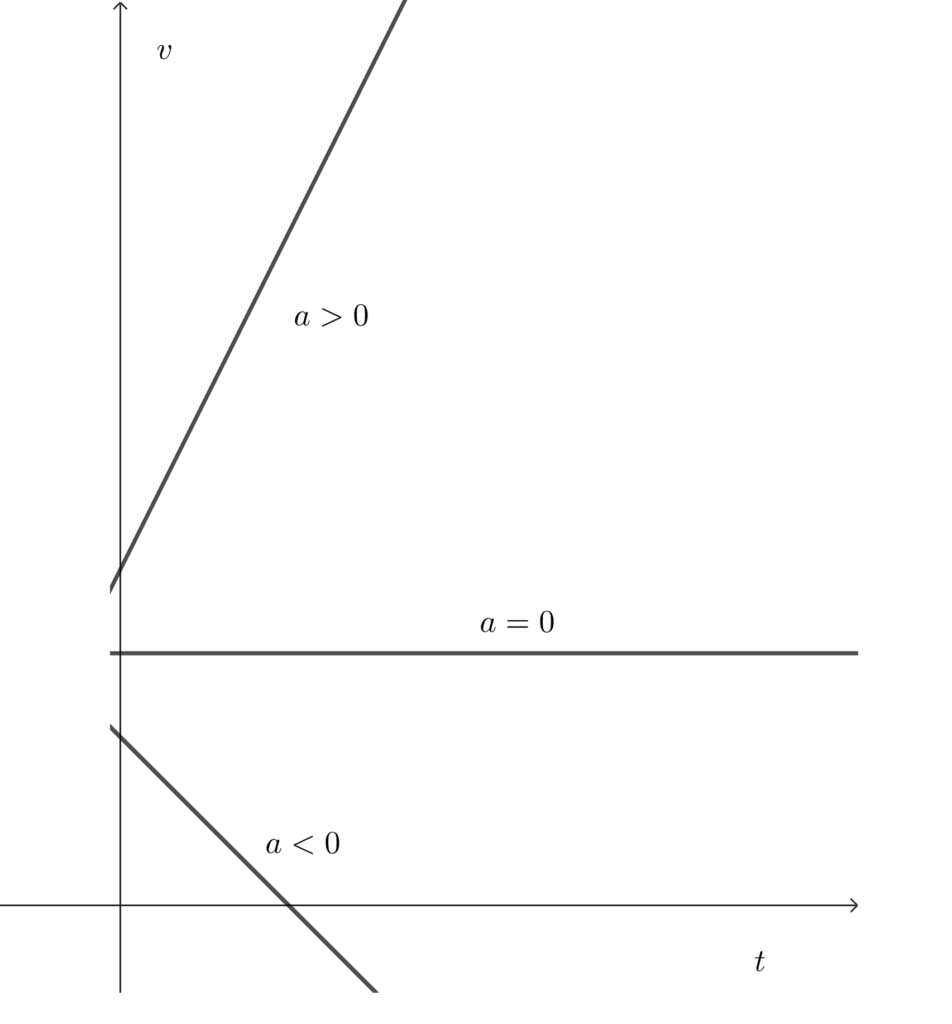
上記\(v-t\)グラフで直線の傾きは加速度の大きさを表しています。加速度の絶対値が大きければ傾きが大きくなり、加速度の絶対値がゼロの時は加速も減速もない状態、つまり等速直線運動となります。
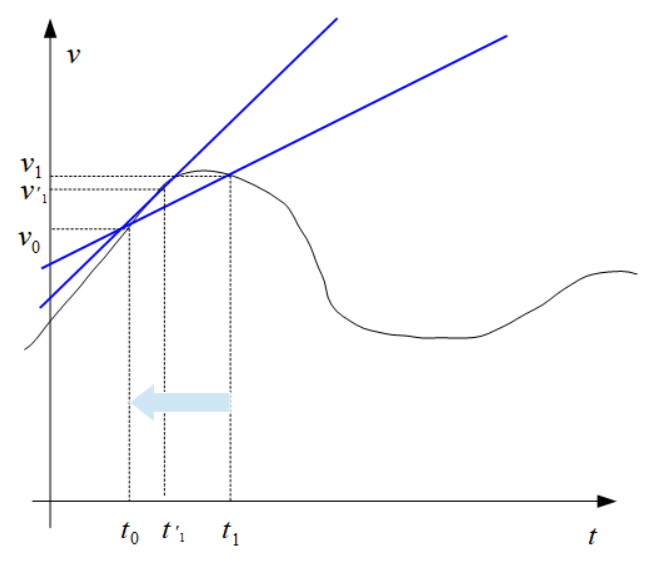
加速度も速度同様、時々刻々と変化するのが普通の自然現象です。したがって、時刻\(t_0\)から\(t_1\)での速度の変化が加速度の定義ですが、これは平均の加速度です。\(t_1\)を限りなく\(t_0\)に近づけていけば\(t_0\)における接線の傾きとなり、この傾きこそが瞬間の加速度を示します。速度同様、瞬間の加速度は \[\large{a=\lim_{\Delta t\to 0}\frac{\Delta v}{\Delta t}=\frac{dv}{dt}}\] と表されます。