等加速度直線運動(1)

加速度が一定の運動のことを等加速度運動といいますが、特に直線上の等加速度運動を等加速度直線運動といいます。
今、直線上を一定の加速度\(a\)m/s²で物体が運動しているときの様子を\(a-t\)グラフで表してみましょう。

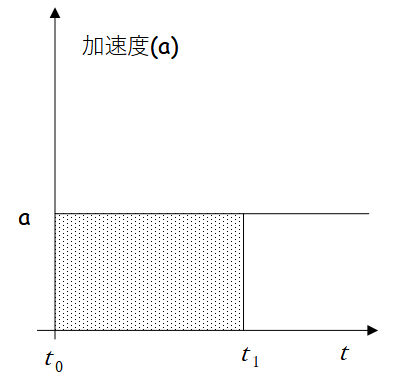
ここで、加速度の定義は \[\large{a=\dfrac{v_1-v_0}{t_1-t_0}}\] だったから、式変形すると \[\large{v_1-v_0=a(t_1-t_0)}\] となるので、上記\(a-t\)グラフの網掛け部分の面積は速度の変化分と等しくなります。このことから \[\large{v=at}\] となり、時刻\(t_0\)における初速度\(v_0\)が与えられている場合は \[\large{v=v_0+at}\] という速度を求める公式が導かれます。

※上記は積分そのものなので\(a\)を時間\(t\)で積分すると\(v\)となることから初速度を\(v_0\)とすると \[v=\int a\ dt=at+v_0\] で導かれます。