等加速度直線運動(6)
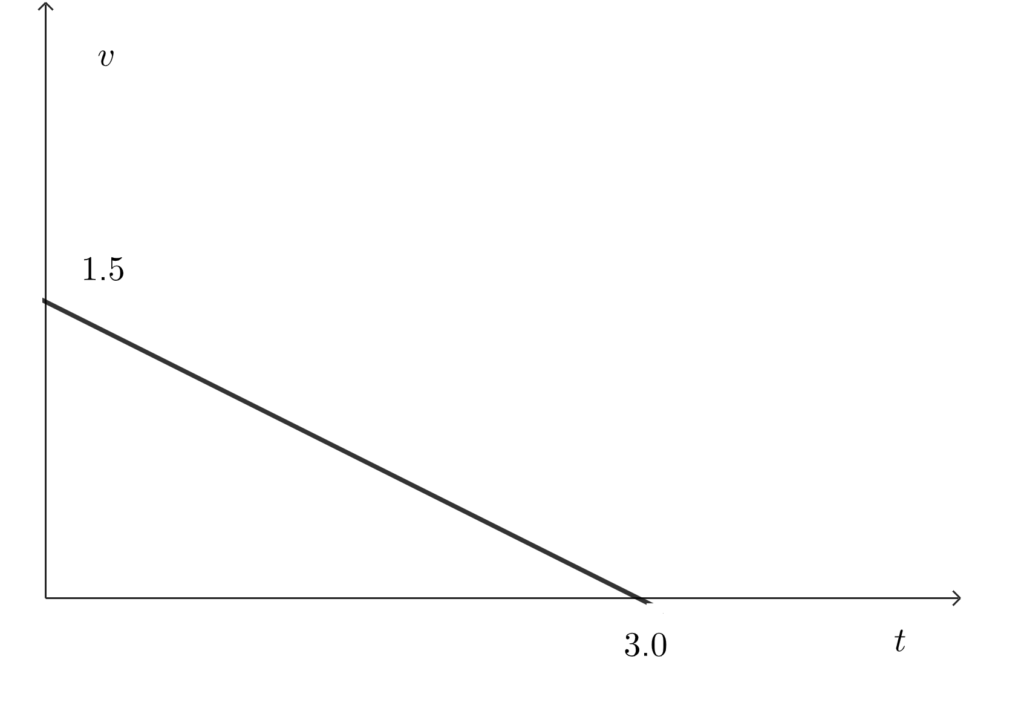
加速度は正の値ばかりとるのではなく、負の値をとることもあります。今、右向きを正として速度1.5m/sで走行する自転車が止まるとき、速度はどんどん遅くなっていくはずです。このときの加速度は速度が徐々に遅くなることから負の加速度をとります。具体的には加速度が-0.5m/s2であったとすると、自転車が止まるまでには\(v=v_0+at\)より \[\large{0.0=1.5-0.5t\\ \therefore t=3.0[s]}\] 3.0秒かかったことになります。この運動の様子を\(v-t\)グラフにすると以下のようになります。
このとき、自転車が止まるまでに走行した距離は、グラフの三角形の面積に等しくなるので、 \[\large{x=\dfrac{1}{2}\cdot 1.5\cdot 3.0=2.25}\] より、2.25m走行したところで停止します。これは等加速度直線運動の公式、\(x=v_0t+\frac{1}{2}at^2\)でも同様に求められ \[\large{x=1.5\cdot 0+\frac{1}{2}\cdot(-0.5)\cdot3.0^2=-2.25}\] という結果となります。変位はベクトルですから、負の値をとっています。自転車が進む方向を正としているため、自転車が進む方向とは逆向きの変位ということを意味します。