自由落下運動(2)

自由落下運動は、重力加速度が一定ですから等速直線運動と基本的には同じ考え方をすることができます。したがって等速直線運動でいう、変位、速度の公式を同様にして求めることが可能です。

前回のおさらいですが、\(g-t\)グラフは重力加速度が一定のため、右のようなグラフとなります。ちなみにいうと、重力加速度は測定する地域によって微妙に違いますので記号\(g\)を使います。数値計算をするときにはその値が与えられています。

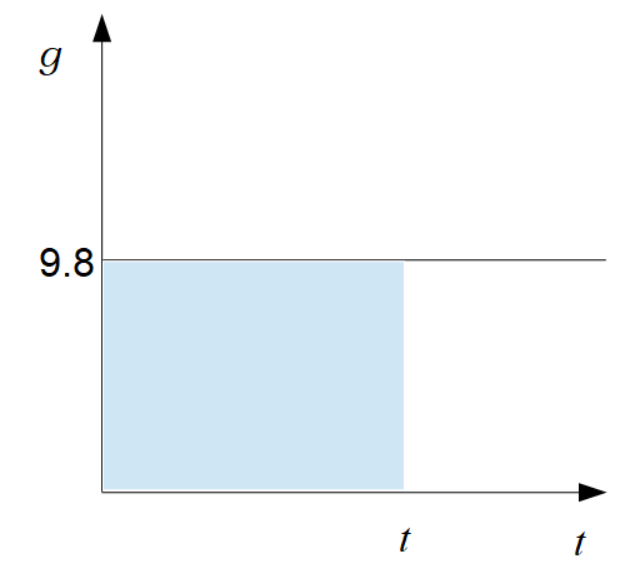
重力加速度は、時間\(t_0\)のときの速度\(v_0\)と時間\(t_1\)のときの速度\(v_1\)の変化の割合に相当します。したがって、 \[\large{g=\frac{v_1-v_0}{t_1-t_0}}\] であらわされます。\(t_0\)と\(t_1\)の差を限りなく0に近づけることによって、 \[\large{g=\frac{\Delta v}{\Delta t}}\] となり、この式を変形すれば \[\large{\Delta v=g\Delta t}\] となるから、上記\(g-t\)グラフの青い部分の面積は速度を表します。要するに \[\large{v=gt}\] の式が導かれます。

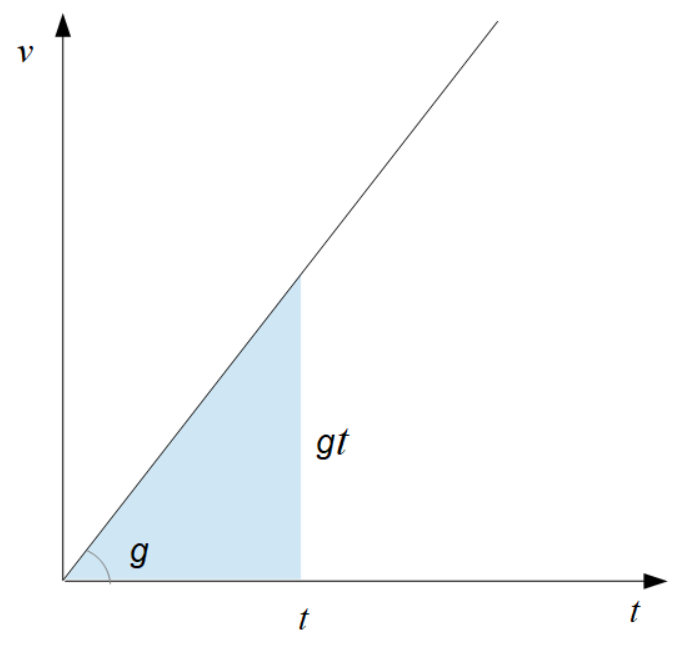
一方、\(v-t\)グラフで、時間\(t\)秒のときの右のグラフが示す三角形の面積は変位を表し、自由落下運動での変位は記号\(y\)を用いて、 \[\large{y=\dfrac{1}{2}gt^2}\] として導けます。