水平投射運動(1)
自由落下、鉛直運動ときたら次は水平投射です。水平投射はその名の通り真横に物体を投げたときの運動のことです。
実際に物体を水平方向に投げてみて、瞬間をカメラで撮影して適当な時間間隔で並べるとわかるのですが、水平方向には等速直線運動、鉛直方向には自由落下運動をしています。
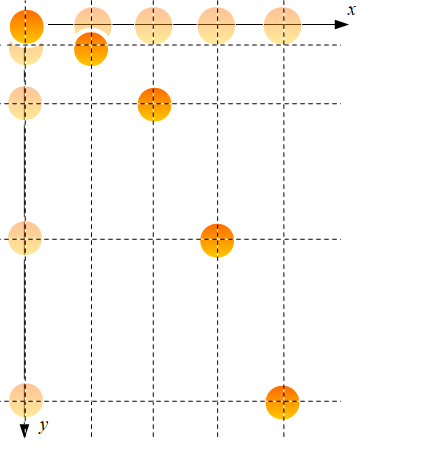
水平右向きを正として\(x\)軸、鉛直下向きを正として\(y\)軸をとると物体は右のような運動をします。
自由落下運動や鉛直運動は1次元である直線上の運動ですが、水平投射運動は水平方向と鉛直方向の2次元上の運動の様子を表します。
2次元上の運動の様子を表す場合、水平方向と鉛直方向に分解して考えるとわかりやすくなります。
そのために、\(x\)軸方向の速度を\(v_x\)、\(y\)軸方向の速度を\(v_y\)として立式していきます。まずは、\(x\)軸方向から考えていきます。\(x\)軸方向は等速直線運動をしていますから、物体の速度と位置は初速度を\(v_0\)とすると、
\[\large{v_x=v_0\\
x=v_0t}\]
で表されます。
一方、鉛直方向は自由落下運動をしますので、初速度は0ですから
\[\large{v_y=gt\\
y=\frac{1}{2}gt^2}\]
で表されます。
ここで、\(x=v_0t\)を変形し、\(t=\dfrac{x}{v_0}\)としたものを\(y=\dfrac{1}{2}gt^2\)に代入すると、
\[\large{y=\dfrac{g}{2v_0^2}x^2}\]
となります。これは水平投射の位置を表す公式です。この式において右辺の\(g\)は重力加速度で一定、初速度\(v_0\)も一定なのでどちらも定数であるから
\[\large{y=(定数)x^2}\]
で表されるので、水平投射は2次関数の放物線を描きます。