静止摩擦力(1)
通常、右のように物体Aを左向きに押そうとしてもなかなか思うようには物体は動いてくれません。これは物体Aと地面に摩擦力がはたらいているからです。「動かない」ということは力がつり合っているからであり、そのつり合っている力は、物体Aを押す力\(F\)と摩擦力\(f\)です。問題文では摩擦力が無視できないような面を「あらい面」といって、摩擦力を無視できる「なめらかな面」と区別しています。
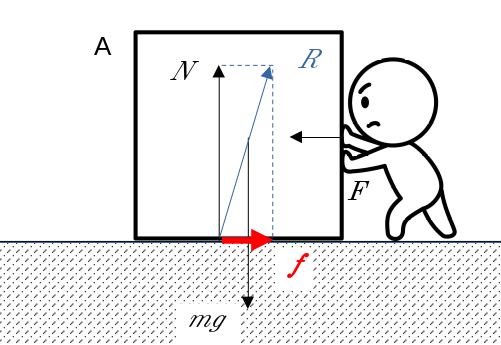
このとき、はたらく力は上図のように、重力\(mg\)、垂直抗力\(N\)、物体を押す力\(F\)の他に物体Aの動きを妨げる方向に摩擦力\(f\)、\(f\)と\(N\)の合力を抗力といい、\(R\)で表しています。静止した物体Aが動くのを妨げる摩擦力を特に静止摩擦力と呼んでいます。
初めは動かなかった物体Aも力\(F\)を大きくしていき、ある大きさを超えるとようやく動き出します。つまり、静止摩擦力にも限界があって、動き出す直前の最も大きい静止摩擦力を最大摩擦力といいます。
最大摩擦力の大きさ\(f_0\)は物体と面とが垂直に押し合う力の大きさである垂直抗力\(N\)に比例し、
\[\large{f_0=\mu_0 N}\]
で表します。なお比例定数\(\mu_0\)を静止摩擦係数といい、接触している面の面積には関係なく接触しある面の種類や状態によって変わります。
物体Aを押す力\(F\)が最大摩擦力\(f_0\)よりも小さい場合は物体Aは静止したままですが、\(F=f_0\)のとき動き出す直前の最大摩擦力となり、\(F\geqq f_0\)、つまり押す力が最大摩擦力以上になると物体Aは動き出します。
