静止摩擦力(3)

今までは平面上に置いた物体に対してのみ取り上げてきましたが、通常はそればかりではありません。今、斜面に物体を置いて角度を少しづつ上げていくと、角度が\(\theta\)のときに物体が滑り始めたときの最大摩擦力を考えます。

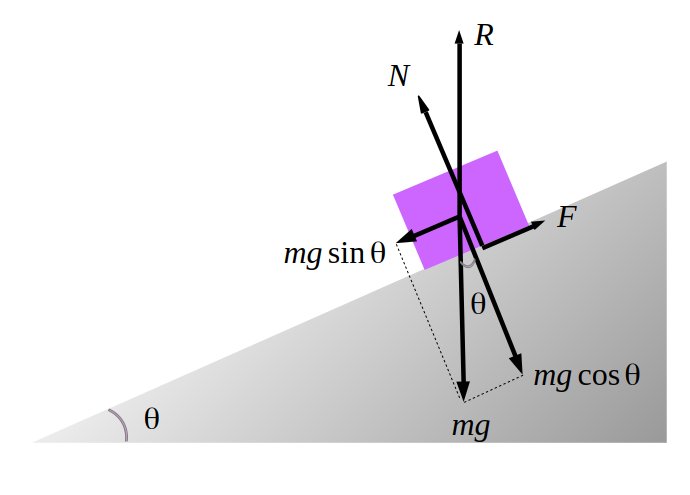
このとき、物体にはたらく力を図示すると上のようになります。

鉛直下向きに重力\(mg\)、鉛直上向きに抗力\(R\)がはたらきますが、鉛直方向には運動しませんので無視します。

次に斜面に平行な力を考えます。重力\(mg\)を斜面に平行な分力と、斜面に垂直な分力に分解します。すると、重力\(mg\)と斜面に垂直な分力のなす角は相似より斜面の角度\(\theta\)と等しくなります。よって、三角比を用いると

斜面に平行な分力・・・\(\large{mg\sin\theta}\)　　斜面に垂直な分力・・・\(\large{mg\cos\theta}\)

となります。ここで角度\(\theta\)のときに斜面下側に滑り始めますから、逆に言うとそれまでの角度では滑らないということです。したがって、摩擦力\(F\)が運動の妨げになる方向、つまり斜面上側にはたらきます。したがって、斜面下側を正とすると

\[\large{mg\sin\theta=F}\]

が成り立ちます。最大摩擦力の公式は\(F_0=\mu_0N\)です。\(N\)は斜面に垂直な向きにはたらく垂直抗力です。斜面に垂直な方向には運動しませんので、垂直抗力\(N\)と逆向きの力である\(mg\cos\theta\)は等しくなります。すなわち

\[\large{N=mg\cos\theta}\]

となるので、これを最大摩擦力の公式に代入、また\(F=mg\sin\theta\)も同様に代入すると

\[\large{mg\sin\theta=\mu_0mg\cos\theta \\ \mu_0=\frac{mg\sin\theta}{mg\cos\theta} \\ \mu_0=\tan\theta}\]

よって、斜面と物体の最大摩擦力は斜面の傾きによって決まることがわかります。