圧力(2)
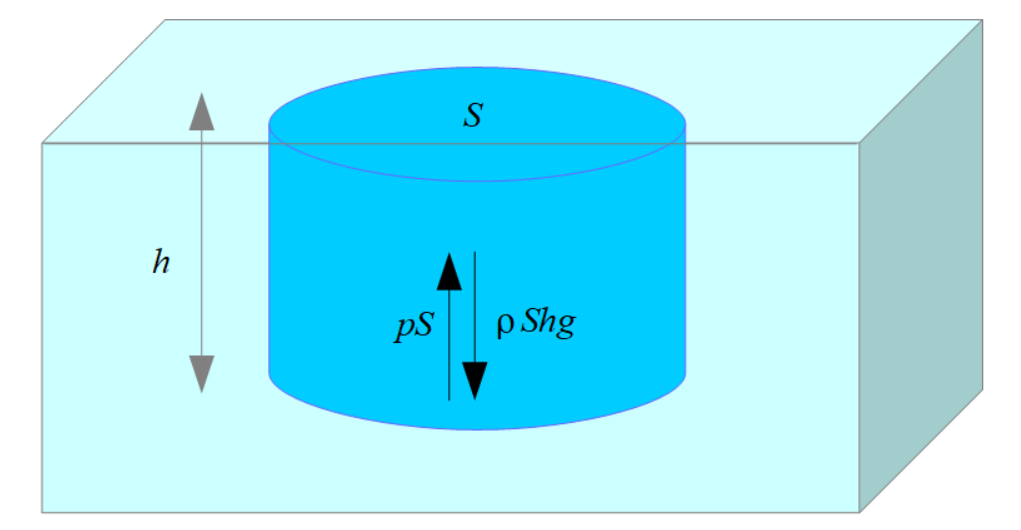
今、水槽に質量\(m\)の円柱状の物体を水面まで沈めて物体が静止したとき、大気圧を考慮しないときの円柱状の物体の底面にかかる水圧を考えてみましょう。物体の高さを\(h\)、底面積を\(S\)とします。
物体には重力がはたらきますので、鉛直下向きに\(mg\)がかかります。そのまま\(mg\)でもいいのですが、それでは深さなどの要素が抜けていますのでうまく変形して入れていきます。水の密度を使っていきます。水の密度\(\rho\)は体積を\(V\)とすると
\[\large{\rho=\frac{m}{V}=\frac{kg}{m^3}}\]
となります。
これでは分母のm\(^3\)が邪魔なのでそれを消すために、底面積\(S\)m\(^2\)と水面からの高さ\(h\)mをかければ、
\[\large{m=\frac{m}{V}Sh=\frac{\text{kg}}{\text{m}^3}\cdot\text{m}^2\cdot\text{m}=\text{kg}}\]
とうまくいきました。ちなみに\(\frac{m}{V}=\rho\)なので、\(mg=\rho gSh\)です。
物体が水を押す上記の力と逆向きに、物体が静止しているため等しい大きさの力(単位:\(N\))が物体の底面から上向きにかかっています。これもうまいこと変形して、物体底面にかかる圧力を\(p\)とすれば底面積\(S\)の関係から
\[\large{pS=\frac{F}{S}\cdot S=\frac{N}{\text{m}^2}\cdot\text{m}^2=N}\]
とすることができるので上向きの力は\(pS\)です。これらが等しいので、
\[\large{pS=\rho gSh \\ p=\rho gh}\]
よって水圧は以下の通り表されます。
\[\large{p=\rho gh}\]
ただし\(\rho:\)水の密度、\(g:\)重力加速度、\(h:\)水面からの高さ
