浮力(3)
Physics問１．密度が\(\rho\)の液体に、密度が\(\rho_0\)、辺の長さが\(\ell \)の立方体を沈めたところ、水深が\(h\)だけ沈んで静止した。このときの水深\(h\)を求めよ。ただし、大気圧を\(P_0\)、重力加速度を\(g\)とする。
静止しているとあるから、上からかかる力と下からかかる浮力はつり合っています。
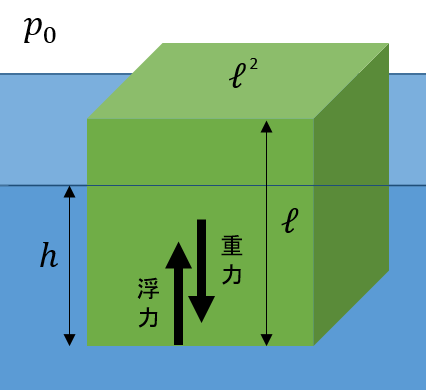
上からの力\(F_{U}\)は大気圧が立方体の面(\(S=\ell ^2\))にかかっていて、立方体だから高さも\(\ell \)より、
\[\large{F_U=P_0+\rho_0 \ell ^3 g}\]
一方、下からの浮力\(F_{D}\)は、水深\(h\)での水圧だから
\[\large{F_{D}=P_0+\rho \ell ^2 h g}\]
ここで物体は静止しているから上下から物体にはたらく力はつり合っているため、
\[\large{F_U=F_D}\]
したがって、
\[\large{P_0+\rho_0 \ell ^3 g = P_0+\rho \ell ^2 h g \\
\therefore h =\underline{h=\frac{\rho_0}{\rho}\ell}}\]
