剛体の運動(2)
壁に立てかけた棒にはたらく力のモーメントを考えてみます。今、あらい床の上に壁に対して角度\(\theta\)で棒を立てかけたとき、棒がすべらずに静止している状況です。棒の長さを\(L\)、棒の質量を\(m\)とします。このときの床に対する摩擦力を求めていく形です。※壁に対しては摩擦力を考えないものとします。
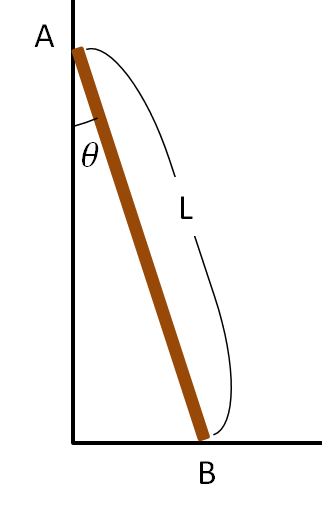
棒にはたらく力を図示すると右のようになります。まず、棒に重力\(mg\)が棒の重心にはたらきます。次に、床からの垂直抗力\(N\)がはたらき、棒を右側にすべらせないための摩擦力\(F\)が床と水平にはたらきます。また、壁からの垂直抗力\(N'\)がこれも床と水平にはたらきます。棒は静止しているのでこれらの力はつり合った状態です。したがって、鉛直方向の力と水平方向の力は等しく
\[\large{\qquad mg=N \cdots(1)\\ \qquad N'=F \cdots(2)}\]
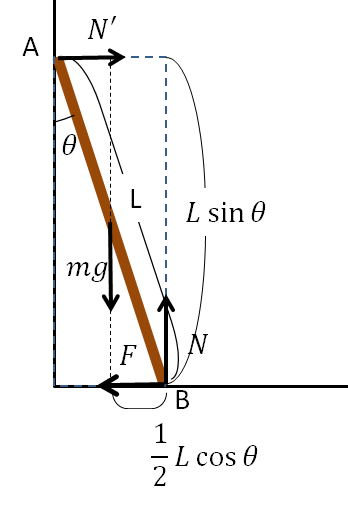
次に力のモーメントのつり合いについてみていきます。Bを回転の軸として\(N',mg\)を右図のように移動してやると、点Aにおける力のモーメントはうでの長さが\(L\sin\theta\)なので\(N'L\cos\theta\)。一方、棒の中点における力のモーメントはうでの長さが\(\dfrac{1}{2}L\cos\theta\)なので\(mg\dfrac{1}{2}L\cos\theta\)。この両者が等しいので
\[\large{N'L\cos\theta=mg\dfrac{1}{2}L\sin\theta\cdots(3)}\]
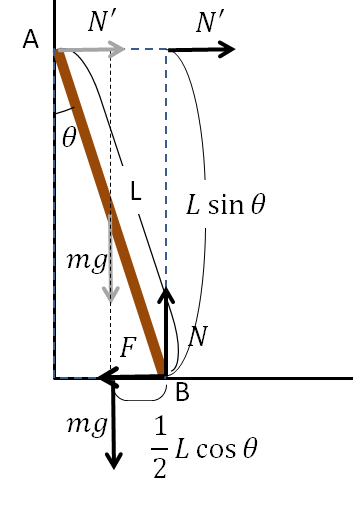
上記3つの式から摩擦力\(F\)を求めます。(3)式より
\[\large{\begin{align} N' &= mg\frac{1}{2}\frac{L\sin\theta}{L\cos\theta} \\ &=\frac{1}{2}mg\tan\theta\end{align}}\]
(2)式より\(N'=F\)のため、
\[\large{\qquad F=\frac{1}{2}mg\tan\theta}\]
であることがわかります。
