力のモーメント(3)

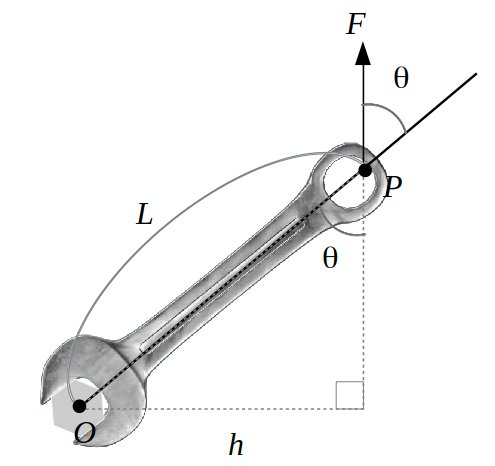
上記のように、ボルトをスパナで緩めるときを考えてみます。今、ボルトの中心を点Oとし、力を加える点を点Pとします。このとき、力\(F\)を矢印の方向に加えると、力のモーメント\(M\)は力と作用線までの距離の積で表されるから

\[\large{M=Fh}\]

となります。ここで、\(h=L\sin\theta\)であるので結局、力のモーメントは以下のとおりとなります。

力のモーメントは回転軸を中心にして反時計回りを正として定義されます。

つまり、回転軸から力の作用点までの距離（＝うでの長さ）と、はたらく力が直角であればその力がそのまま回転させる力としてはたらくことになります。ここから力のモーメントの別の求め方として、作用点におけるうでの長さと直角方向の力の成分を用いる方法もあります。以下のように、力\(F\)をうでの長さに垂直成分と並行成分に分解します。

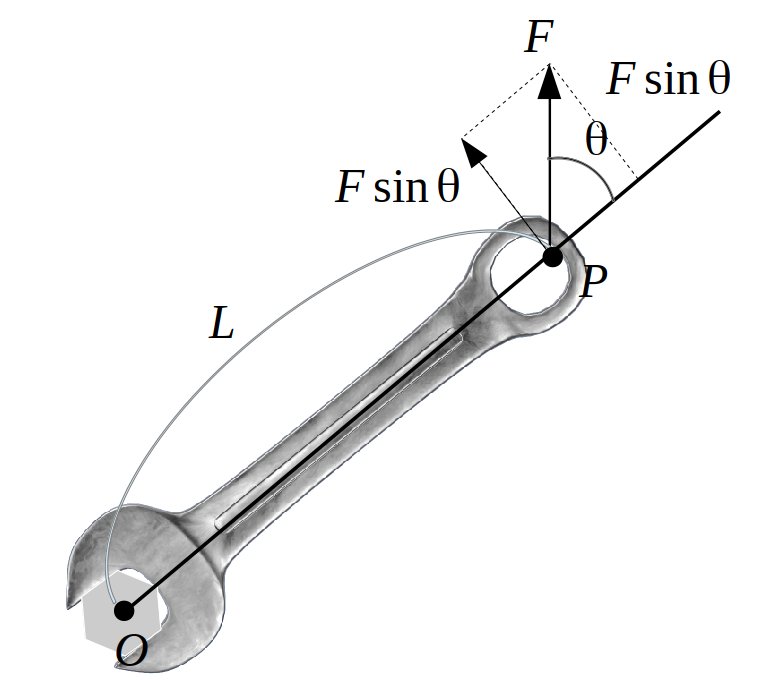
力のモーメントは力と作用線までの距離（＝うでの長さ）の積だから

\[\large{M=F\sin\theta L=FL\sin\theta}\]

となって、式としては変わりません。