力のモーメント(5)
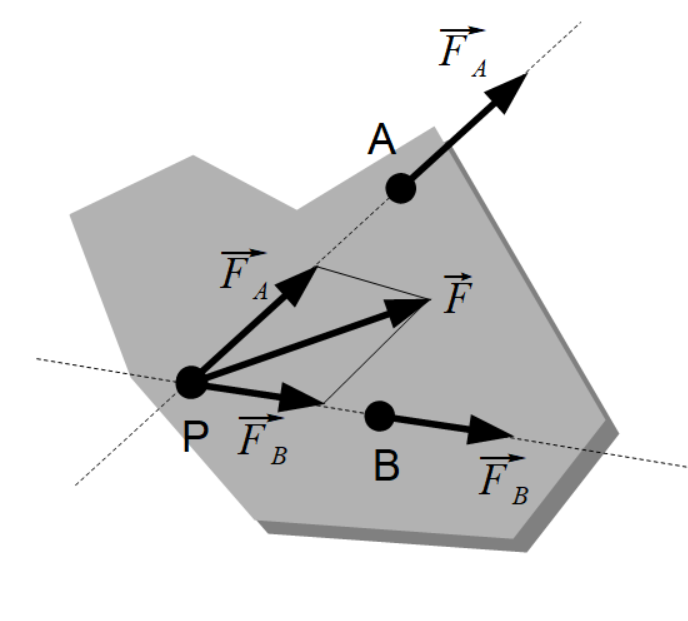
右のように物体に平行でない力\(\overrightarrow{F_A},\overrightarrow{F_B}\)がはたらいているときの、2力の合力\(\overrightarrow{F}\)を求めます。それには、それぞれの力の作用点A、Bを各力の作用線の交点まで移動させ、平行四辺形の法則により合力\(\overrightarrow{F}\)が求められます。ベクトルは向きと大きささえ変わらなければ同じもの、という性質を利用したものとなります。
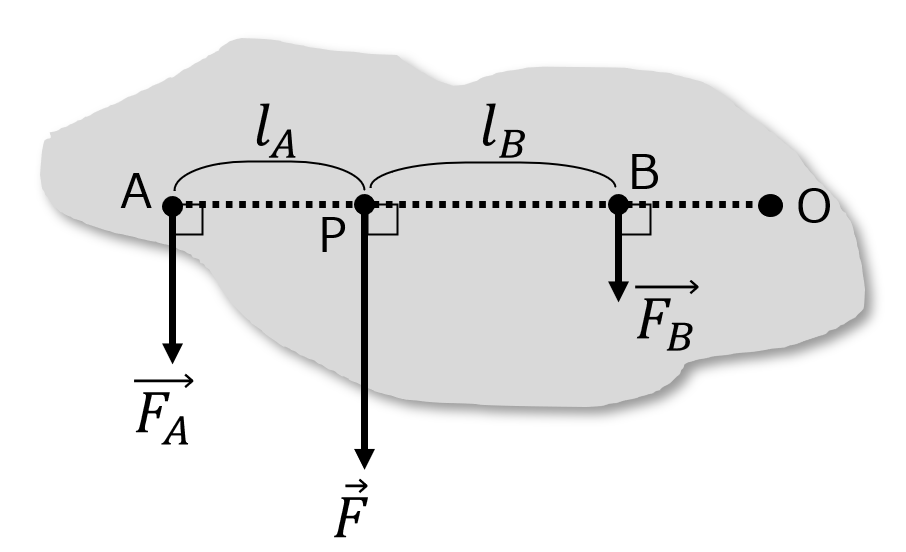
では、右のように2つの力\(\overrightarrow{F_A},\overrightarrow{F_B}\)がはたらいているときの合力\(\overrightarrow{F}\)はどのようになるでしょうか。
まず、ABの延長線上に任意の点Oをとり、合力\(\overrightarrow{F}\)の作用点をPとします。点Oを回転軸とする\(\overrightarrow{F_A},\overrightarrow{F_B}\)の力のモーメントの和は合力\(\overrightarrow{F}\)の力のモーメントと等しくなければならないことを踏まえて、\(\overrightarrow{F_A},\overrightarrow{F_B}\)および\(\overrightarrow{F}\)の力の大きさを\(F_A,F_B,F\)とすると、
\[\large{F_A\times(\text{AP+PO})+F_B\times\text{BO}=F\times\text{PO}}\tag{1}\]
ここで、\(F_A,F_B\)の合力が\(F\)であることおよびそれらの向きは同じことから、
\[\large{F=F_A+F_B}\]
したがって、(1)式は
\[\large{F_A\times(\text{AP+PO})+F_B\times\text{PO-PB}=(F_A+F_B)\times\text{PO}\\ F_A\times\text{AP}=F_B\times\text{PB}}\]
よって、AP=\(l_A\)、PB=\(l_B\)とすると、
\[\large{\text{AP:PB}=l_A:l_B=F_B:F_A=\frac{1}{F_A}:\frac{1}{F_B} \\ \because a:b=c:d \iff ac=bd}\]
ここから、一般的に平行で同じ向きの2力の合力の作用線は、元の2力の作用点間を力の大きさの逆比に内分する点を通り、合力の大きさは2力の大きさの和となり、その向きは元の2力と同じ向きとなります。