力のモーメント(6)

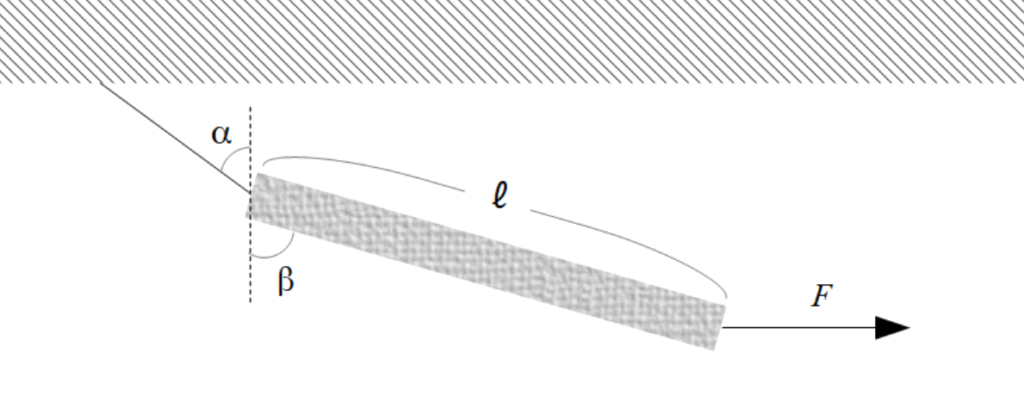
棒が静止したとあるので、並進方向および回転方向の力はつり合っていることになります。まずは並進方向の力のつり合いについて考えます。その前に、棒にかかっている力を図示します。糸の張力を\(T\)とすると、

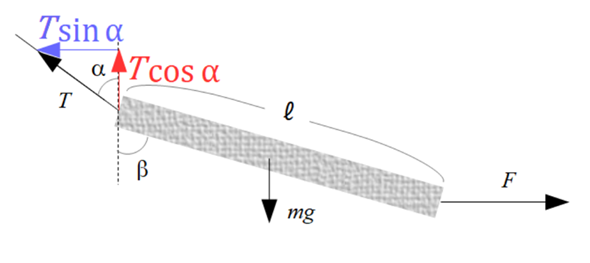
ここから力のつり合いは
鉛直方向：\(\large{T\cos\alpha=mg}\tag{1}\)
水平方向：\(\large{T\sin\alpha=F}\tag{2}\)
(2)式を(1)式で割ると、 \[\large{\qquad\frac{T\sin\alpha}{T\cos\alpha}=\frac{F}{mg} \\ \qquad\tan\alpha=\frac{F}{mg}}\tag{3}\] 次に、回転方向の力のつり合い、つまり力のモーメントについて考えます。回転の中心は糸と棒の接点とし、これを点Oとしておきます。
うでの長さを図示すると以下のようになります。

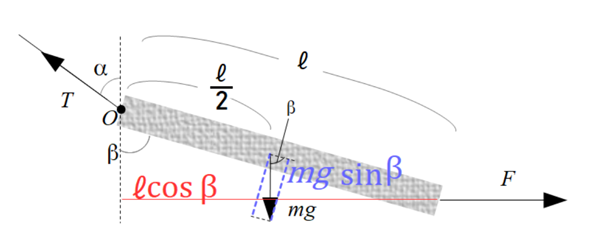
これらがつり合っているので、 \[\large{\qquad F\ell\cos\beta=\frac{\ell }{2}mg\sin\beta }\tag{4}\] (4)式の両辺を\(\ell\cos\beta\)で割ると、 \[\large{\qquad F=\frac{1}{2}mg\tan\beta \\ \qquad \frac{F}{mg}=\frac{1}{2}\tan\beta}\tag{5}\] ここで、(3)式より\(\dfrac{F}{mg}=\tan\alpha\)であるから \[\large{\qquad\tan\alpha=\frac{1}{2}\tan\beta \\ \qquad 2\tan\alpha=\tan\beta}\] ＜終＞