重心(1)

今、質量が\(m_1\)の物体と\(m_2\)の物体が同一直線上に配置されており、点Oからの距離がそれぞれ\(x_1,x_2\)であるとします。このとき、これら2物体は静止しているとします。

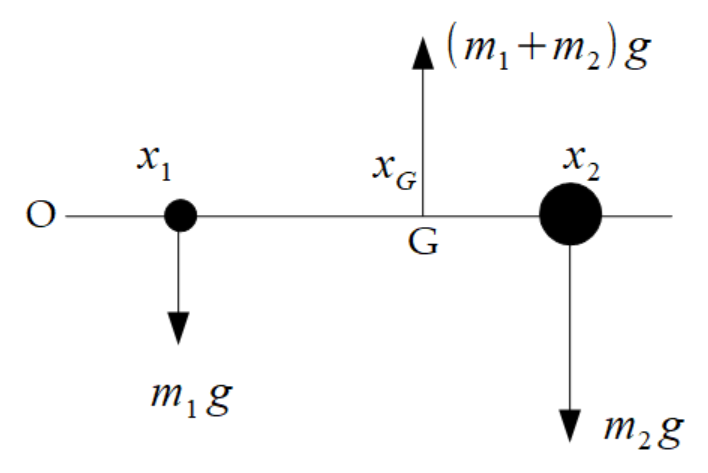
静止しているということは、上向きに\((m_1+m_2)g\)がはたらいていないといけません。その力がはたらいている点を重心といい、ここではGと表し点Oからの距離を\(x_G\)とします。ちなみに重心は重力を考慮した２物体間の中心という意味合いで、必ずしも２物体間の距離の中心ではありません。

ここで、その重心Gの位置を求めるのが今回の主題です。点Gを回転の中心として、力のモーメントを求めると

\[\large{(m_1+m_2)g\times 0+m_1g(x_G-x_1)-m_2g(x_2-x_G)=0 \\ \therefore m_1g(x_G-x_1)=m_2g(x_2-x_G)}\]

上記式を\(g\)で割って整理すると

\[\large{m_1(x_G-x_1)=m_2(x_2-x_G) \\ m_1x_G+m_2x_G=m_1x_1+m_2x_2 \\ \therefore x_G=\frac{m_1x_1+m_2x_2}{m_1+m_2}}\]

これが重心\(x_G\)の位置となります。