重心(3)

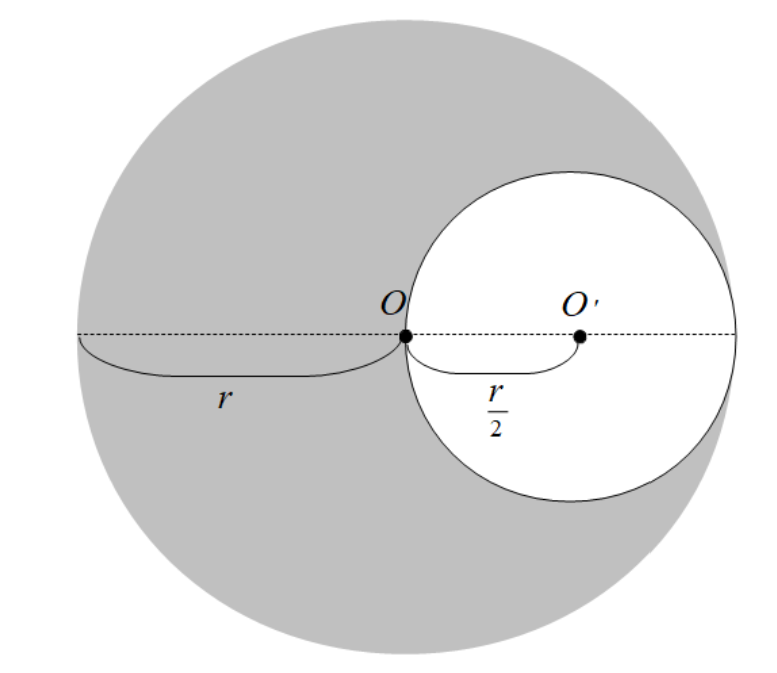
（１）くりぬく前のの円の面積は\(\pi r^2\)。くりぬいた円の面積は\(\pi\left(\dfrac{r}{2}\right)^2=\dfrac{\pi r^2}{4}\)。よって、くりぬいた部分の面積を1とすればくりぬく前の面積はその4倍となるので1:4。問題はくりぬいた後の部分の面積なので\(4-1=3\)だから \[\large{\underline{1:3}}\] （２）くりぬいた円を元に戻すことを考えると、そのくりぬいた円の重心は\(O'\)です。また、くりぬかれて残った部分の重心はわかりませんが、仮に\(G\)としておきます。すると、それぞれの重心にかかる質量も、以下のように1:3となります。

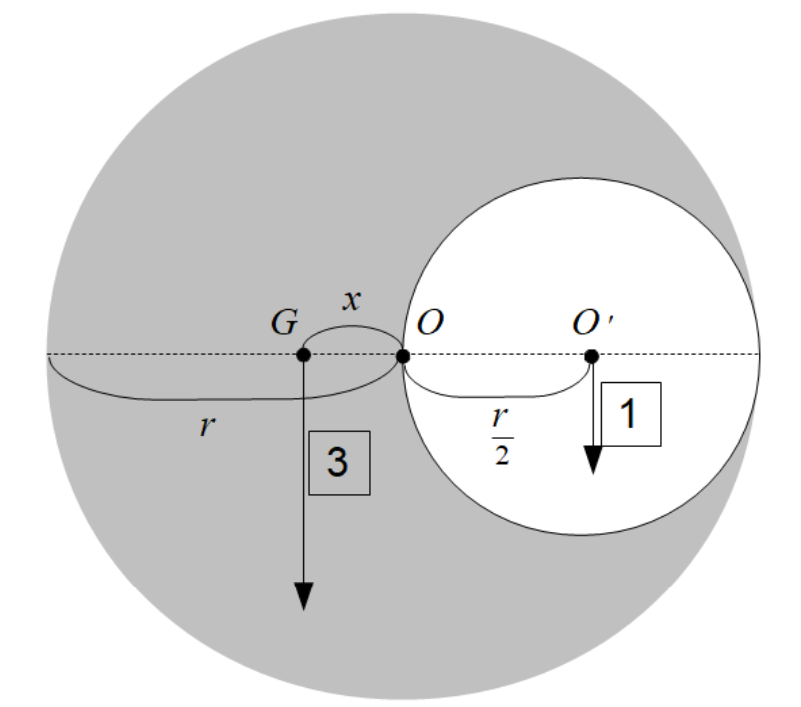
ここまでくれば後は力のモーメントの考えを適用すればよく、点Oを回転の中心とすると \[\large{3x=\frac{r}{2} \\ \therefore \underline{x=\frac{r}{6}}}\] となります。つまり、点Oから\(\dfrac{r}{6}\)左側の位置となります。