物体が倒れない条件(1)
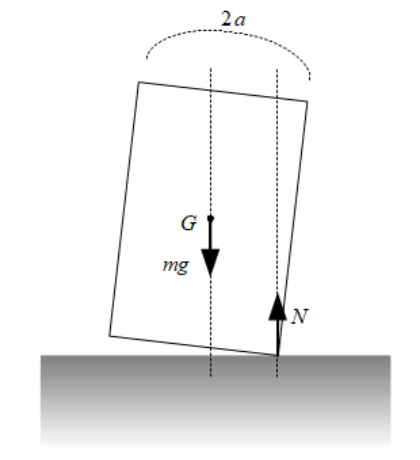
横の長さが\(2a\)の物体を徐々に傾けていくといずれ倒れてしまいます。当たり前の話ですが、どの時点で倒れるとわかるのでしょうか。今、荒い床に物体を置いて、右側に傾けていくことを想定します。
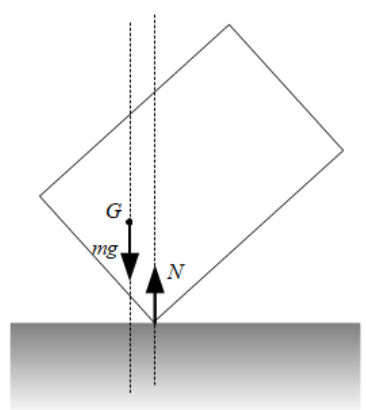
重心は傾けても位置は変わらず、重心から鉛直下向きに重力\(mg\)がかかります。一方、垂直抗力は床と接している部分にかかります。このとき、重力と垂直抗力の作用線が異なるため、力のモーメントの和が0とならず、左側に回転するため元に戻ります。
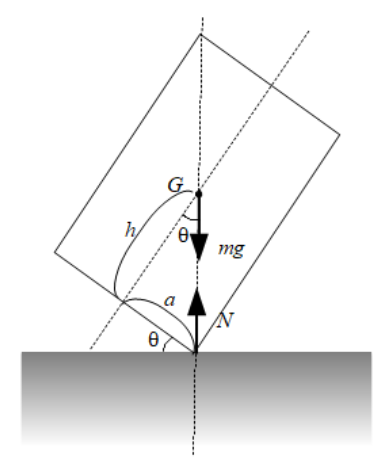
中央の図では重力と垂直抗力の作用線が等しくなるため、この角度で物体は静止しますが少しでも角度がずれるとどちらかに回転してしまいます。
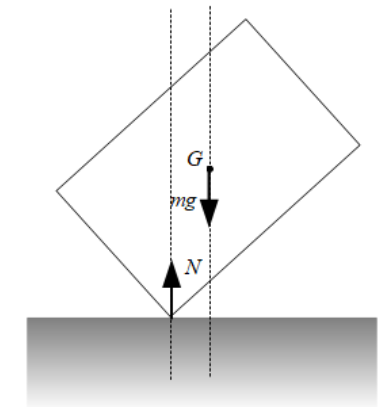
さらに右側に傾けていくと、右図のように重力の作用線よりも垂直抗力の作用線が左側にきており、とうとう右側に倒れてしまいます。
中央の図のように、倒れずに静止したときの状態で考えてみます。物体の底面から重心までの高さを\(h\)、右側に傾けた角度を\(\theta\)とすると、
\[\large{\tan\theta=\frac{a}{h}}\]
のとき倒れないことがわかります。
このことから、\(h\)が大きい(=重心が高い)ほど小さい角度で倒れてしまうことがわかります。逆に言えば\(h\)が小さい(=重心が低い)ほど角度が大きくても倒れにくいことがわかります。
つまり、防災上の面から物体の重心を低くすることが、物体が倒れることによる被害を抑えることができます。下に重いものを、上に軽いものを置くようにすれば、重心が低くなり倒れにくくなります。