仕事の正負(2)
問1.水平方向となす角度が30°のあらい斜面に質量10kgのタイヤを50m回転させた。このとき、タイヤには斜面から5.0Nの一定の動摩擦力を受けた。重力加速度を9.8m/s2とするとき、以下の問いに答えよ。
(1)重力が物体にした仕事を求めよ。
(2)垂直抗力が物体にした仕事を求めよ。
(3)摩擦力が物体にした仕事を求めよ。
(4)物体が50m落下するまでに受けた仕事を求めよ。
まず物体にはたらく力を図示します。垂直抗力を\(N\)、重力を\(mg\)、摩擦力を\(f\)とします。
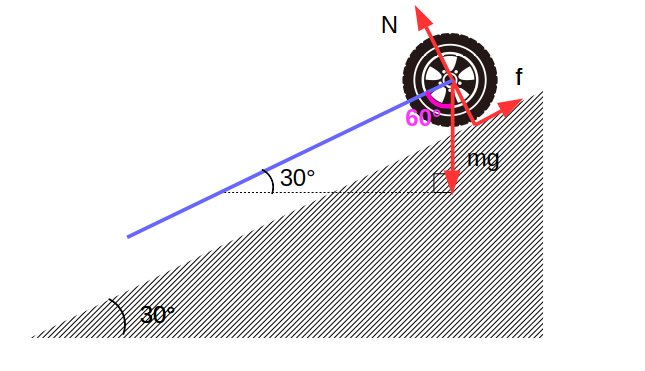
(1)重力は鉛直方向にはたらきます。仕事の公式\(W=Fx\cos\theta\)より、\(F=mg=10\times9.8\)、\(x=50\)、\(\theta=60°\)より、仕事\(W\)は
\[\large{\begin{align}
W &= Fx\cos\theta \\
&= 10\times9.8\times50\times\cos60° \\
&= \underline{4.9\times10^3[J]}\end{align}}\]
(2)垂直抗力は変位に対して常に垂直です。したがって、物体に対して仕事はしていません。よって、仕事は\(\large{\underline{0[J]}}\)。
(3)
仕事の公式\(W=Fx\cos\theta\)より、\(F=f=5.0\)、\(x=50\)、\(\theta=180°\)より、仕事\(W\)は
\[\large{\begin{align}
W &= Fx\cos\theta \\
&= 5.0\times50\times\cos180° \\
&= \underline{-2.5\times10^2[J]}\end{align}}\]
(4)物体が50m落下するまでに受ける力は、重力・垂直抗力・摩擦力なので、それらから受けた仕事の和を求めればよいです。よって、
\[\large{\begin{align}
W &= 4.9\times10^3+0+(-2.5\times10^2) \\
&= \underline{5.2\times10^3[J]}\end{align}}\]
