仕事の原理(1)
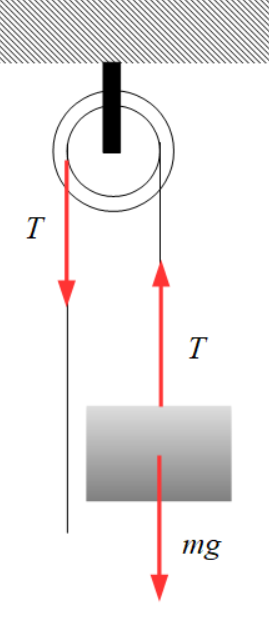
質量が\(m\)[kg]の物体を摩擦や質量を無視できる定滑車でゆっくりと\(h\)[m]だけ引き上げるときのことを考えます。糸の質量を無視すれば、力を図示すると右のようになり、
\[\large{T=mg}\]
となるから、\(h\)[m]引き上げたければ張力\(T\)に\(h\)[m]引き上げるだけの力を加えればよい。よって、このときの仕事\(W_1\)は
\[\large{W_1=Th}\]
となります。
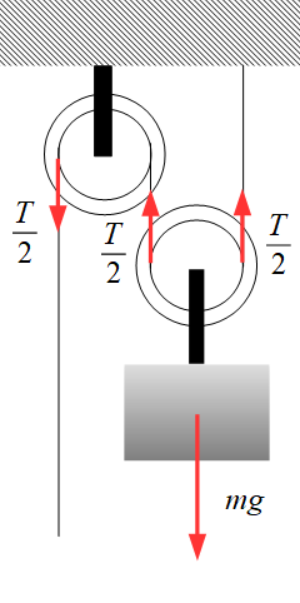
同様に質量\(mg\)の物体を摩擦や質量を無視できる動滑車でゆっくりと\(h\)[m]だけ引き上げるときのことを考えます。力を図示すると右のようになります。このとき、\(mg\)とつり合う張力は2つの糸の張力となるので、\(\dfrac{T}{2}\)となり下に引く張力も\(\dfrac{T}{2}\)となります。このとき、物体を\(h\)[m]引き上げるとすれば
\[\large{\dfrac{T}{2}=h \\ T=2h}\]
分の距離を引かなければなりません。つまり、張力そのものは定滑車の半分で済みますが、引く距離は物体を持ち上げる距離の2倍が必要ということです。このときの仕事\(W_2\)は
\[\large{W_2=\dfrac{T}{2}\times 2h =Th}\]
です。ここで、\(W_1=W_2\)であり、定滑車でも動滑車でも、もっと言えば人力でも仕事の大きさは変りません。このことを仕事の原理と呼んでいます。