仕事率(2)
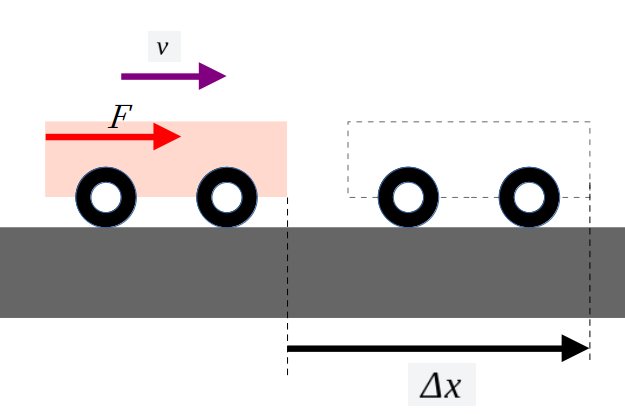
物体を床面に置いて右側に大きさ\(F\)[N]の力を与えて、力の向きに速さ\(v\)[m/s]で運動し始めたときの仕事率を求めてみましょう。
微小時間\(\Delta t\)[s]の間に、物体に一定の\(F\)[N]の力を与えつつ移動した距離を\(\Delta x\)[m]とします。この微小時間に加えた力のした仕事は
\[\large{W=F\Delta x}\]
です。
ということで、仕事率は
\[\large{P=\frac{F\Delta x}{\Delta t}}\]
です。一方、この微小時間における物体の速さは
\[\large{v=\frac{\Delta x}{\Delta t}}\]
ですから、仕事率\(P=\dfrac{F\Delta x}{\Delta t}\)の式を変形して、
\[\large{P=Fv}\]
となります。この導出により、\(P=Fv\)は速さ\(v\)で動いている物体の瞬間の仕事率を示し、\(P=\dfrac{W}{t}\)は時間\(t\)での平均の仕事率を示していることがわかります。
