物体が倒れない条件(2)
問1.質量が\(m\)の一様な物体を荒い床におき、右上隅に力\(F\)を水平右向きに徐々に加えていく。このとき、以下の問いに答えよ。ただし、重力加速度を\(g\)、床と物体の静止摩擦係数を\(\mu_0\)とする。
(1)物体が静止しているときの垂直抗力の作用点の、点Oからの距離を求めよ。
(2)物体が傾くより先にすべり出したときの、力\(F\)の大きさを求めよ。
(3)物体がすべり出すより先に傾いたときの、力\(F\)の大きさを求めよ。
(4)物体が傾くより先にすべり出すときの条件を求めよ。
(1)物体にかかっている力を図示します。
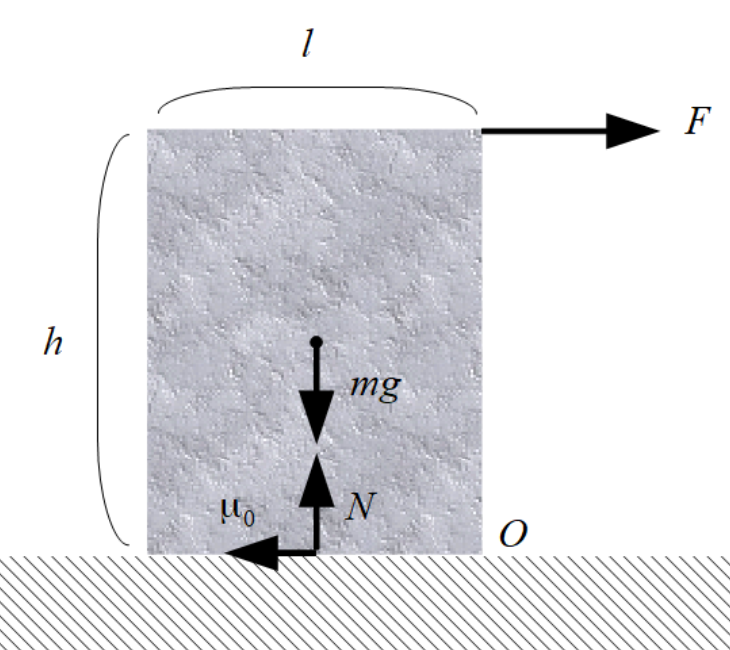
ここで、点Oを中心とする力のモーメントを求めます。
右上隅にかかる力のモーメント(時計回り):\(\large{Fh}\)
垂直抗力に対する力のモーメント。点Oからの距離を\(d\)とする(時計回り):\(\large{Nd=mgd}\)
重力に対する力のモーメント(反時計回り):\(\large{\dfrac{l}{2}mg}\)
静止しているということから、反時計回りを正とすると力のモーメントの和は0になるので、
\[\large{\dfrac{l}{2}mg-Fh-mgd=0}\]
より、\(d\)を求めると、
\[\large{\qquad mgd=\dfrac{l}{2}mg-Fh \\ \qquad d=\underline{\frac{l}{2}-\frac{Fh}{mg}}}\]
(2)すべり出すということは、力Fの方が最大静止摩擦力よりも大きくなるときです。最大静止摩擦力は\(\mu_0 mg\)なので
\[\large{\underline{F > \mu_0 mg}}\]
(3) (1)から、問題文から与えられていない情報である\(d\)が変数となります。この\(d\)が負となると\(\dfrac{l}{2}mg-Fh-mgd=0\)の\(-mgd\)が正となってしまい和が0でなくなり傾いてしまいます。よって、
\[\large{\qquad 0>\frac{l}{2}-\frac{Fh}{mg} \\
\qquad\frac{Fh}{mg} > \frac{l}{2} \\
\qquad Fh > \frac{lmg}{2} \\
\qquad \underline{F > \frac{lmg}{2h}}}\]
(4)(3)より、\(d>0\)であれば傾きません。よって、
\[\large{F < \frac{lmg}{2h}}\tag{1}\]
また、(2)よりすべり出す条件は
\[\large{F > \mu_0 mg}\tag{2}\]
(1)(2)式より、
\[\large{\underline{\mu_0 mg < F < \frac{lmg}{2h}}}\]
