仕事の正負(1)
右図のように、物体を水平方向に\(x\)m移動させるとき、力の方向が水平方向と角度\(\theta\)をなすとすれば、力の物体に対する仕事は、
\[\large{W=Fx\cos\theta}\]
で表されます。
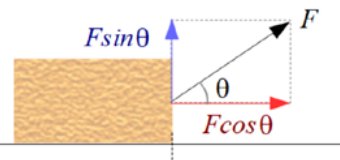
ここで、\(\theta\)の範囲を\(0°\leqq\theta < 90°\)とすれば、\(\cos\theta > 0\)であるから、仕事の値は常に正の値を取ります。
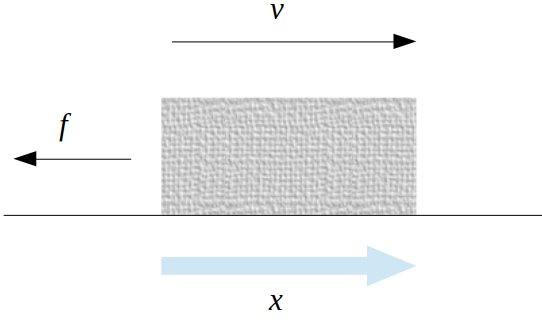
ここで、\(\theta\)の値が\(90° < \theta\leqq180°\)の場合、運動を妨げる方向に力がはたらきます。このとき、\(\cos\theta\)の値は負になるため、力が物体にする仕事は負になります。
左の図のように、なめらかな床面に右方向に運動している物体があって、左方向に一定の力\(f\)[N]を加え、\(x\)m変位したとき、仕事は
\[\large{W=fx\cos180°=-fx}\]
となります。
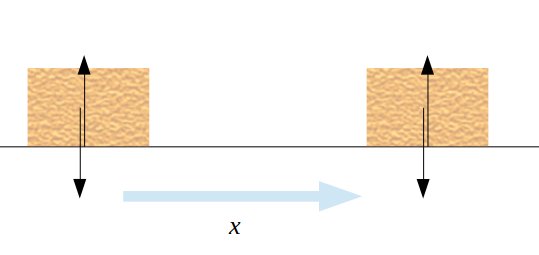
また、\(\theta=90°\)のとき、\(\cos90°=0\)となります。そのため、運動の方向が水平方向のとき、上下方向の力(垂直抗力・重力)は変位量に影響を与えないので、仕事は0となります。
一般に、物体に2つ以上の力がはたらいているとき、それらの合力のする仕事は、それぞれの力がする仕事の和に等しくなります。