相対速度(4)

車Aの速度を\(\overrightarrow{v_{A}}\)、車Bの速度を\(\overrightarrow{v_{B}}\)とすると、車Bに対する車Aの相対速度\(\overrightarrow{v_{AB}}\)は \[\large{\begin{align} \overrightarrow{v_{AB}} &= \overrightarrow{v_{A}}-\overrightarrow{v_{B}} \\ &= 10\text{[m/s]}-12\text{[m/s]} \\ &= \underline{-2\text{[m/s]}}\end{align}}\]

状況を模式的に表すと以下のようになります。


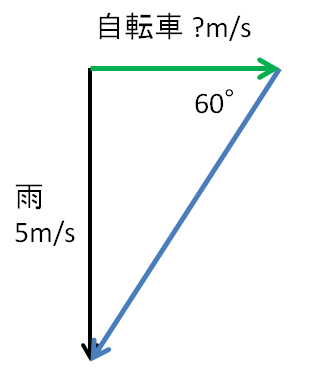
これは60°、30°、90°の直角三角形です。つまり、辺の比は\(1:2:\sqrt{3}\)です。このことから車の速度を\(x\)[m/s]とすれば \[\large{1:\sqrt{3}=x:5.0 \\ x = \frac{5.0}{\sqrt{3}} = 2.9 }\] したがって自転車の速度は\(\large{\underline{2.9\text{[m/s]}}}\)。