等加速度直線運動(2)
次に等加速度直線運動の様子を\(v-t\)グラフで表してみます。
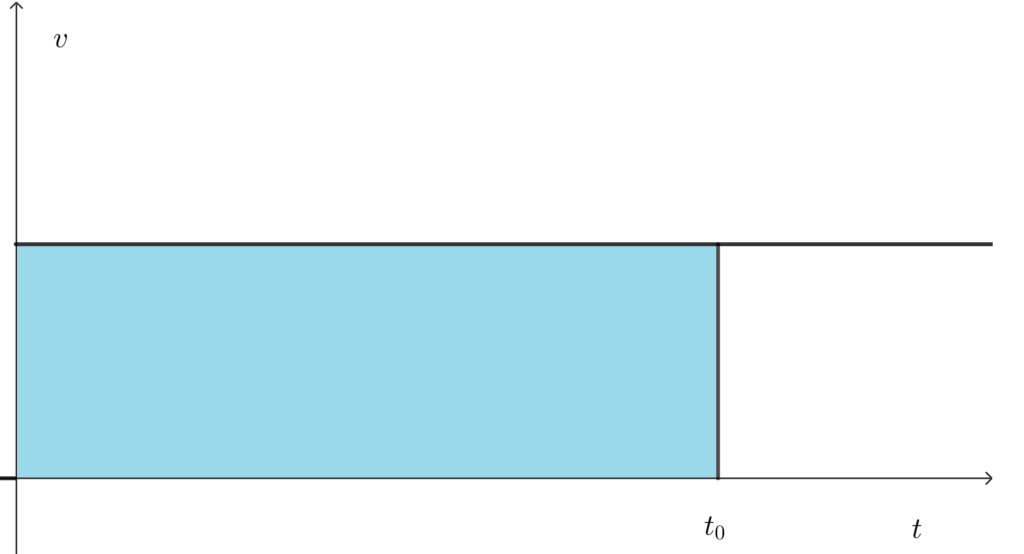
その前に等速直線運動は速度が変わらない運動、すなわち加速度が0の運動なので右図のように\(v\)が\(t\)軸に対して平行な直線となります。
このときの水色の領域の面積は変位を表していました。
ここで、加速度\(a=2\)[m/s2]のときの速度の変化の様子を表にしてみます。\(t=0\)のときの速度は0[m/s]とします。
| 時間\(t(s)\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
|---|---|---|---|---|---|---|---|---|
| 速度\(v\)(m/s) | 0 | 2 | 4 | 6 | 8 | 10 | 12 | … |
この表から\(v-t\)グラフを作成すると以下の通りとなります。
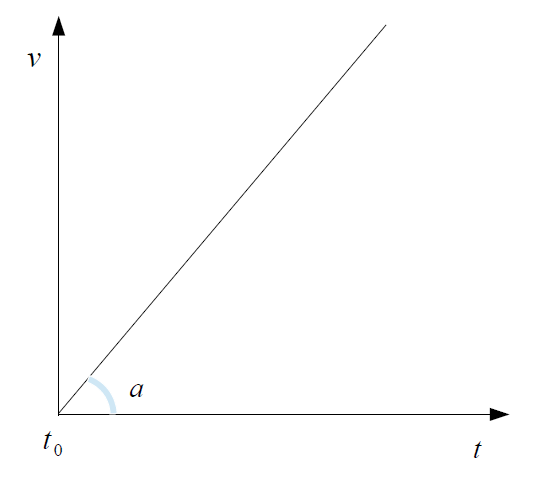
このとき、直線の傾きは加速度\(a=2\)[m/s2]を表すので直線の方程式は \[\large{v=at}\] で表されます。この式は前回でも別の方法で導かれた式です。
ここで初速度\(v_0=1\)[m/s]が与えられているとすると、そのときの速度の様子は以下の通りとなってきます。
| 時間\(t(s)\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
|---|---|---|---|---|---|---|---|---|
| 速度\(v\)(m/s) | 1 | 3 | 5 | 7 | 9 | 11 | 13 | … |
この表から\(v-t\)グラフを作成すると以下のような1次関数の直線 \[\large{v=v_0+at}\] となります。
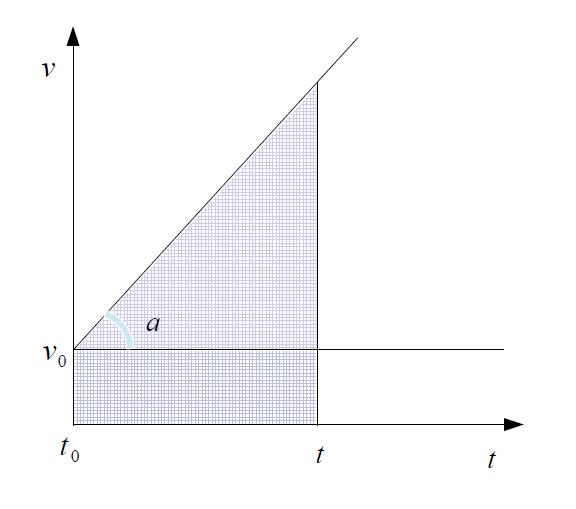
\(v-t\)グラフの表す直線と\(t\)軸で囲まれた図形の面積が変位を表すのは変わりません。よって、変位\(x\)は上記グラフの網掛けの部分の台形の面積に相当し、 \[\large{x=\dfrac{1}{2}at^2+v_0t}\] で表されます。特に\(t_0\)のときの変位を\(x_0\)とすれば \[\large{x=\dfrac{1}{2}at^2+v_0t+x_0}\]となります。
※積分で表すと、速度を積分すると変位となることから \[\begin{align} x &= \int v dt \\ &= \int (v_0+at) dt \\ &= \frac{1}{2}at^2+v_0t+C\end{align}\] \(t_0\)のときの変位を\(x_0\)とすると、 \[x=\frac{1}{2}at^2+v_0t+x_0\]
