等加速度直線運動(8)
問5.初速度2.0m/sで右向きに走行する自動車が時刻\(t=0.0\)[s]から一定の加速度で減速し、完全に停止するまで40m走行した。
(1)減速しているときの加速度を求めよ。
(2)自動車が減速し始めてから完全に停止するまでの時間を求めよ。
問6.時刻\(t=\)0.0[s]から\(t=\)2.0[s]まで右向きに速度0.10m/sで等速直線運動をする小球が時刻\(t=\)2.0[s]から一定の加速度で減速し始めてから完全に停止するまで10[s]を要した。
(1)小球が運動している様子を\(v-t\)グラフで表せ。
(2)小球が減速しているときの加速度を求めよ。
(3)小球が\(t=\)0.0[s]から完全に停止するまで移動した距離を求めよ。
(1)減速しているときの加速度を求めよ。
(2)自動車が減速し始めてから完全に停止するまでの時間を求めよ。
(1)\(v^2-V_0^2=2ax\)より
\[\large{0.0^2-2.0^2=2a\cdot 40 \\
\therefore a=\underline{-0.05[\text{m/s}^2]}}\]
(2)\(v=v_0+at\)より
\[\large{0.0=2.0-0.05t \\
\therefore t=\underline{40[\text{s}]}}\]
問6.時刻\(t=\)0.0[s]から\(t=\)2.0[s]まで右向きに速度0.10m/sで等速直線運動をする小球が時刻\(t=\)2.0[s]から一定の加速度で減速し始めてから完全に停止するまで10[s]を要した。
(1)小球が運動している様子を\(v-t\)グラフで表せ。
(2)小球が減速しているときの加速度を求めよ。
(3)小球が\(t=\)0.0[s]から完全に停止するまで移動した距離を求めよ。
(1)以下の通り。
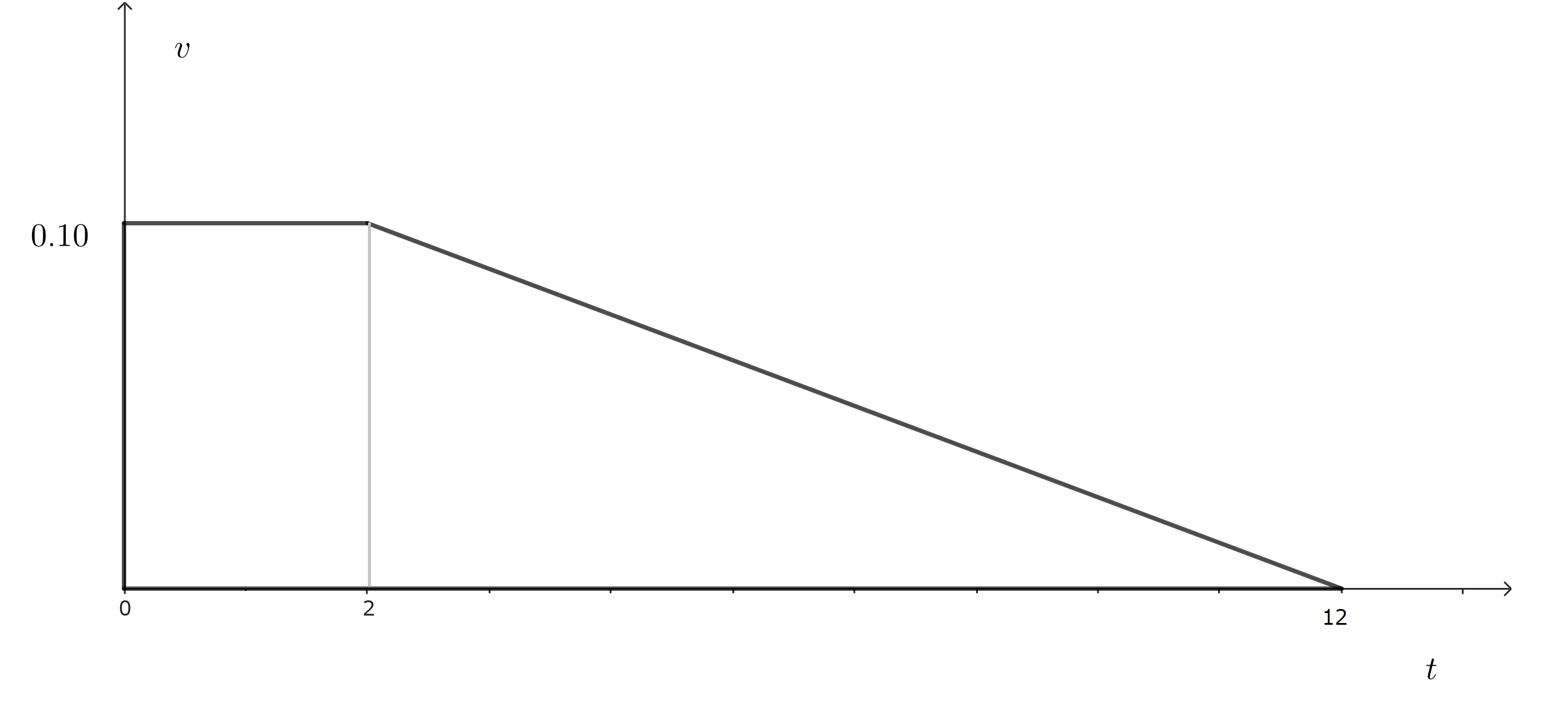
(2)10[s]間に速度が0.10m/sから0.0m/sに変化していることから、
\[\large{a=\frac{0.0-0.10}{12-2}=\underline{-0.01[\text{m/s}^2]}}\]
※または、\(v=v_0+at\)より\(0.0=0.1+10a\)から求めても結果は同じ。
(3)距離は\(v-t\)グラフの面積に相当しますから
\[\large{x=\frac{1}{2}\times(2.0+12)\times 0.10=\underline{0.70[\text{m}]}}\]
