鉛直投げ上げ運動(1)

投げ下ろしとくれば次は投げ上げです。つまり、鉛直上方に初速度をもって投げ上げて、重力に伴って落ちてくるという運動です。基本的には投げ下ろし運動と似ていますが、よく考えないと間違うポイントもあります。

通常、座標をとるときには上を正としてとりますが、鉛直投げ下ろし運動の場合は鉛直下向きを正として座標をとりましたが鉛直投げ上げ運動は基本に立ち返って鉛直上向きを正とします。

重力加速度は常に鉛直下向きに働きますから、鉛直上向きを正としているので鉛直投げ上げ運動においては負の値をとることになります。したがって、重力加速度\(g\)は\(-g\)として扱わなければなりません。

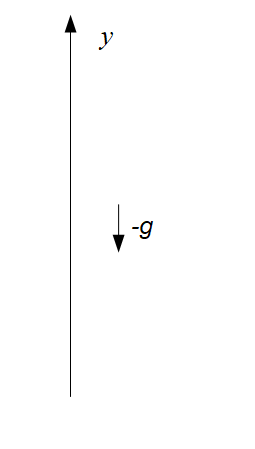
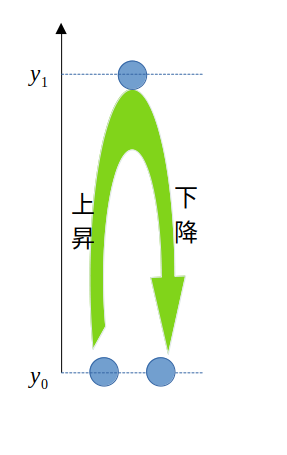
地点\(y_0\)から初速度\(v_0\)で鉛直上方に投げ上げたボールは最高地点\(y_1\)まで上昇したあと下降に転じ（自由落下運動となる）、地点\(y_0\)まで戻ってくる運動を行います。

投げ上げたボールは徐々に速度が減少し、最高地点\(y_1\)で一瞬速度が0になったあと、自由落下運動のため重力加速度にしたがって徐々に速度を増しながら\(y_0\)まで落下します。