水平投射運動(2)
水平投射運動の速度を考えてみます。それには水平方向と鉛直方向の速度を合成して考えます。速度はベクトルですから水平方向の速度を\(\overrightarrow{v_x}\)、鉛直方向の速度を\(\overrightarrow{v_y}\)として、水平投射の物体の運動の様子に書き込むと以下のようになります。
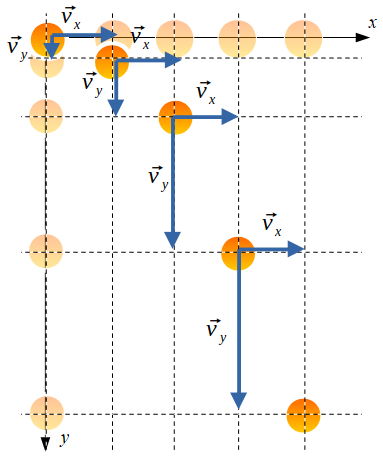
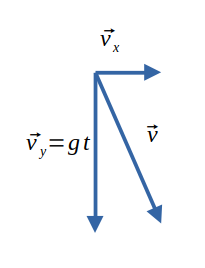
この\(\overrightarrow{v_x},\overrightarrow{v_y}\)の合成速度が\(\overrightarrow{v}\)となります。\(\overrightarrow{v}\)の大きさは三平方の定理より
\[\large{\overrightarrow{v}=\sqrt{\overrightarrow{v_x}^2+\overrightarrow{v_y}^2}}\]
また、鉛直下向きの速度は自由落下運動を示し、\(\overrightarrow{v_y}=gt\)より
\[\large{\overrightarrow{v}=\sqrt{\overrightarrow{v_x}^2+(gt)^2}}\]
と表すことができます。時刻\(t\)における加速度の大きさはその定義より
\[\large{a=\frac{\Delta\overrightarrow{v}}{\Delta t}}\]