力の合成・分解(2)

同一作用線上に2つの力がはたらいていない場合は、それぞれの力の大きさを1辺とする平行四辺形を描き、その対角線をその2つの力の合力とします。

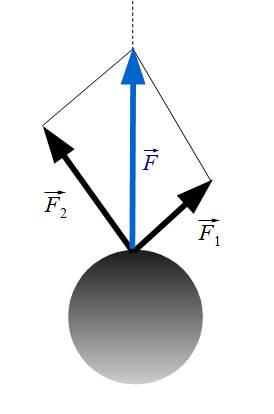
右の図のように力\(\overrightarrow{F_1},\overrightarrow{F_2}\)が物体にはたらいているときは、\(\overrightarrow{F_1},\overrightarrow{F_2}\)が作る平行四辺形の対角線が合力\(\overrightarrow{F}\)となります。

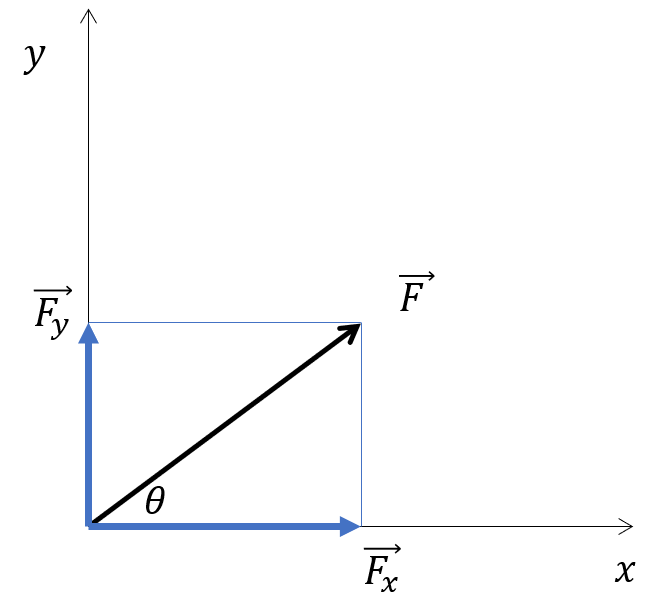
右の図のように\(\overrightarrow{F}\)を\(x\)軸、\(y\)軸方向へ分解した分力はそれぞれ\(\overrightarrow{F_x},\overrightarrow{F_y}\)になります。

\(\overrightarrow{F}\)と\(x\)軸のなす角を\(\theta\)とすると、 \[\large{\begin{align} \overrightarrow{F_x} &= \overrightarrow{F}\cos\theta \\ \overrightarrow{F_y} &= \overrightarrow{F}\sin\theta\end{align}}\] で表すことができます。また、三平方の定理により、 \[\large{\overrightarrow{F}=\sqrt{\overrightarrow{F_x}+\overrightarrow{F_y}}}\] となります。

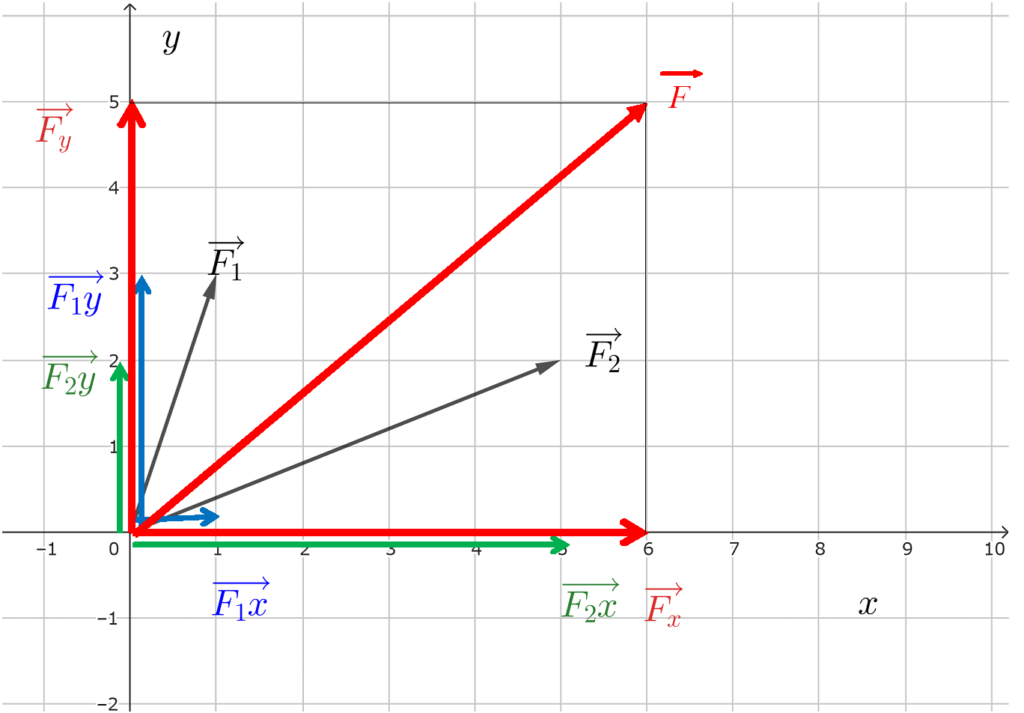
2つの力\(\overrightarrow{F_1},\overrightarrow{F_2}\)の合力は以下のように求められます。

\(\overrightarrow{F_1},\overrightarrow{F_2}\)の\(x,y\)成分をそれぞれ \[\large{\qquad \overrightarrow{F_1}=(\overrightarrow{F_{1x}},\overrightarrow{F_{1y}}) \\ \qquad \overrightarrow{F_2}=(\overrightarrow{F_{2x}},\overrightarrow{F_{2y}})}\] とすると、2つの力の\(x,y\)成分の和\(\overrightarrow{F_x},\overrightarrow{F_y}\)は以下のようになります。 \[\large{\qquad \overrightarrow{F_x}=\overrightarrow{F_{1x}}+\overrightarrow{F_{2x}} \\ \qquad \overrightarrow{F_y}=\overrightarrow{F_{1y}}+\overrightarrow{F_{2y}}}\] したがって、\(\overrightarrow{F_1},\overrightarrow{F_2}\)の合力\(\overrightarrow{F}\)は \[\large{\overrightarrow{F}=\overrightarrow{F_x}+\overrightarrow{F_y}}\] となります。