力の合成・分解(3)
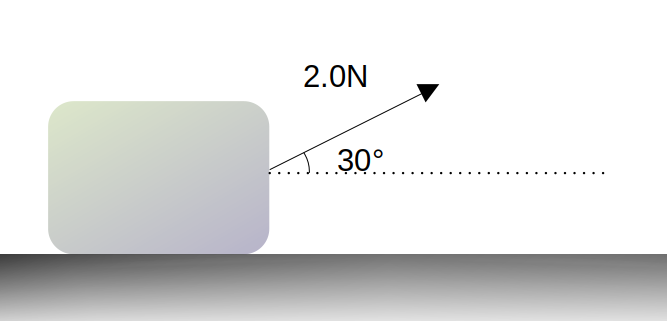
問1.以下のように物体を水平方向とのなす角が30°の方向に2.0[N]の力で引っ張った。このとき、水平方向には何Nの力が加えられているか求めよ。ただし\(\sqrt{3}=1.7\)とする。
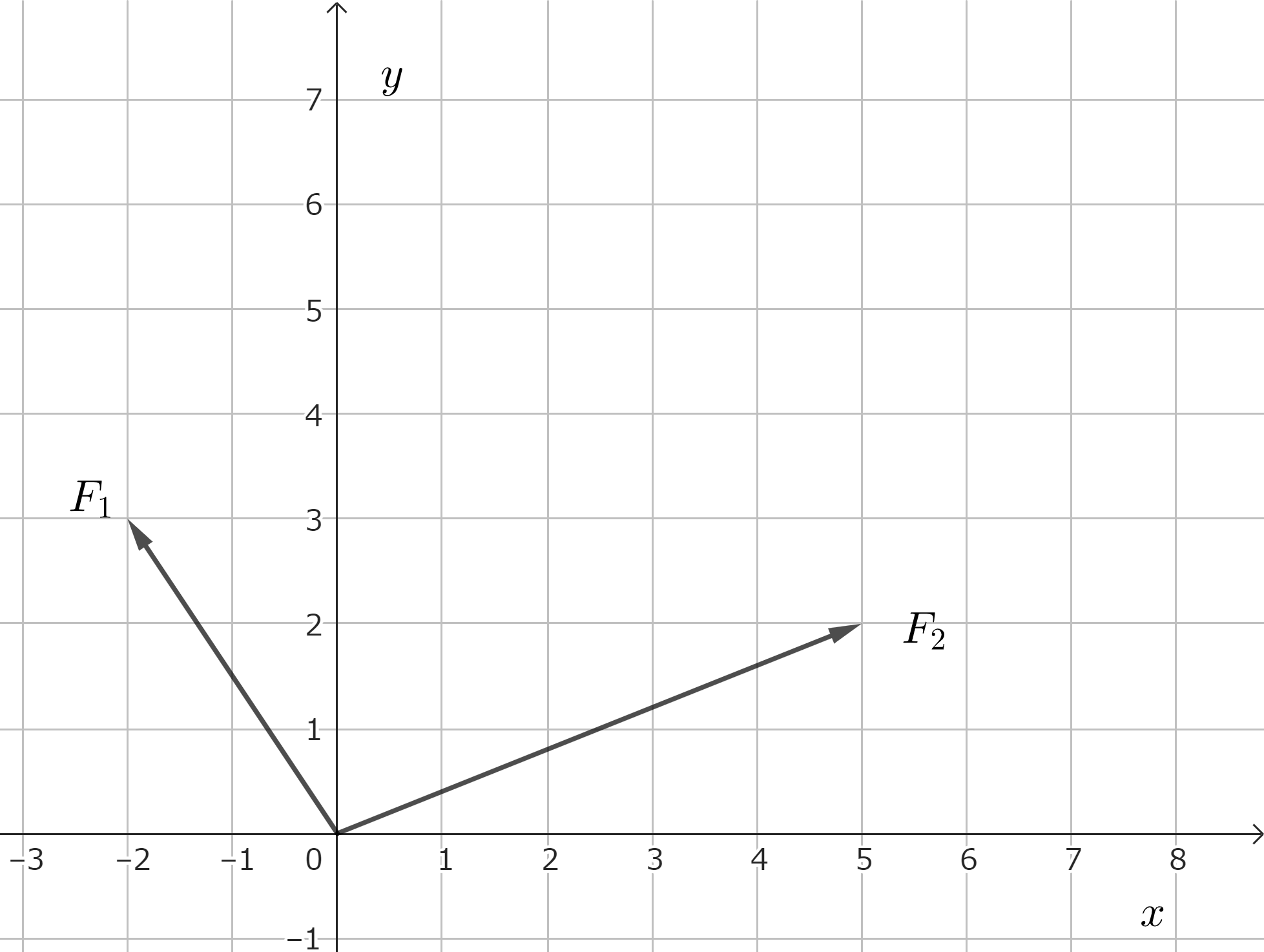
問2.以下のように2つの力\(\overrightarrow{F_1},\overrightarrow{F_2}\)があるとき、\(x\)軸、\(y\)軸方向の力と、\(\overrightarrow{F_1},\overrightarrow{F_2}\)の合力\(\overrightarrow{F}\)を作図せよ。

水平方向の力を\(F_x\)とすれば
\[\large{\qquad\cos 30°=\frac{F_x}{2.0} \\
\qquad\therefore F_x=2.0\cos30°}\]
三平方の定理より、\(\cos 30°=\dfrac{\sqrt{3}}{2}\)。したがって、
\(F_x=2.0\times\dfrac{\sqrt{3}}{2}=\sqrt{3}=\large{\underline{1.7[\text{N}]}}\)。
問2.以下のように2つの力\(\overrightarrow{F_1},\overrightarrow{F_2}\)があるとき、\(x\)軸、\(y\)軸方向の力と、\(\overrightarrow{F_1},\overrightarrow{F_2}\)の合力\(\overrightarrow{F}\)を作図せよ。

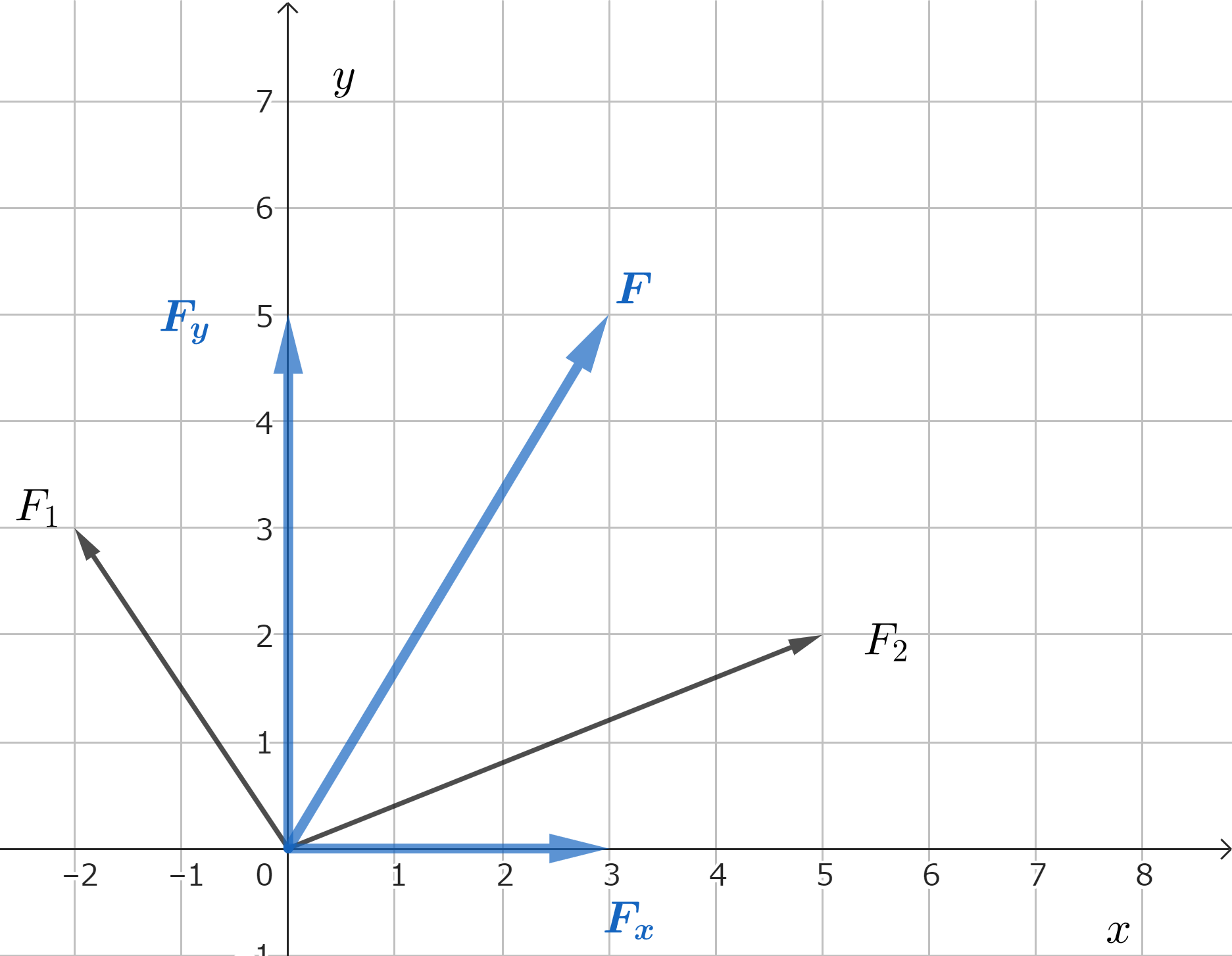
\(F_1=(-2,3),F_2=(5,2)\)より、
\[\large{F_x=-2+5=3 \\
F_y=3+2=5}\]
よって、合力\(\overrightarrow{F}\)は以下の通り。