運動方程式(2)

運動方程式\(ma=F\)より \[\large{3.0\times 1.5=4.5}\] したがって、右向きに4.5N

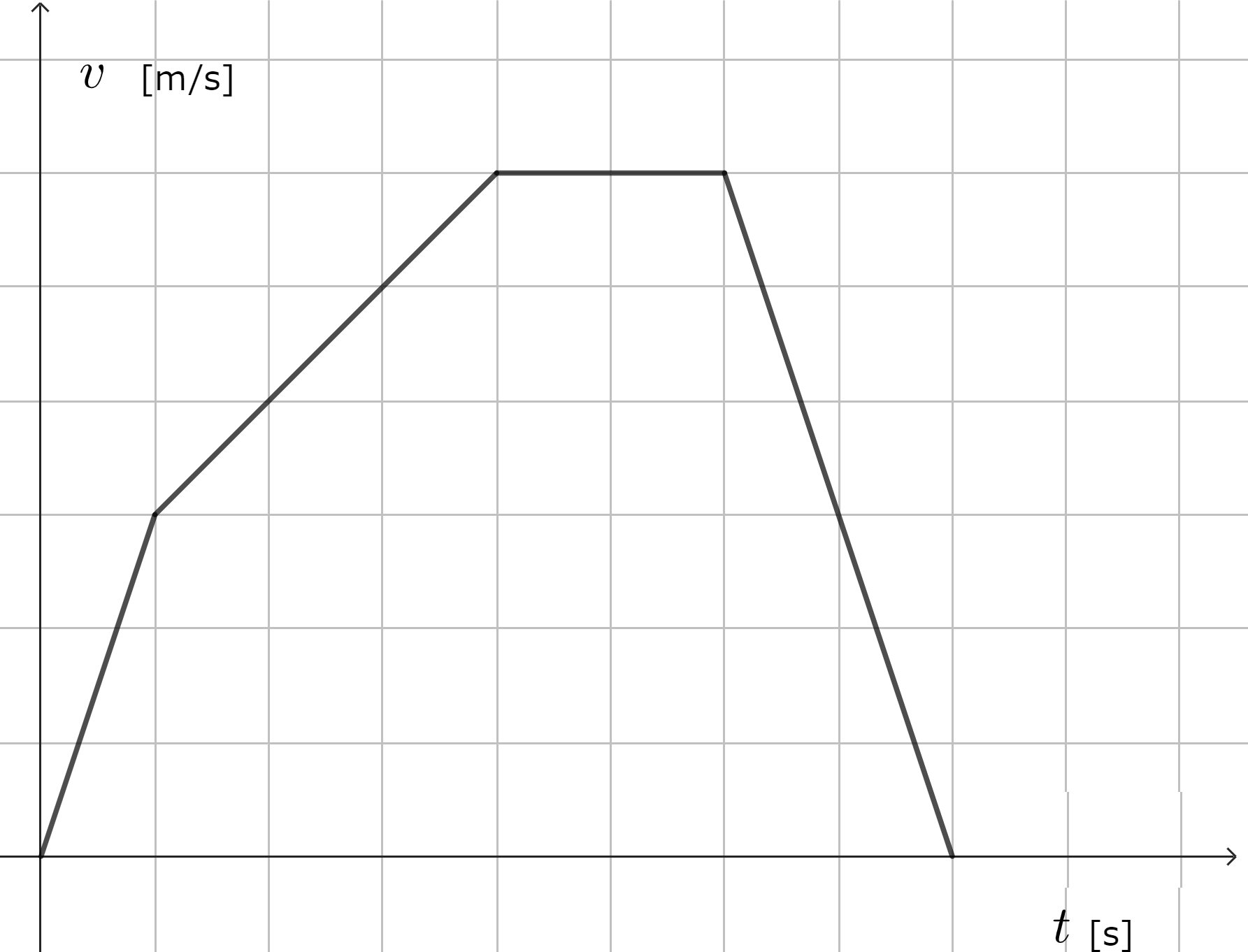
（１）「物体が動き始めたとき」というのは\(t=0.0\)から\(t=1.0\)間の等加速度直線運動をしているときです。このときの加速度は \[\large{a=\frac{3.0-0.0}{1.0-0.0}=3.0[\text{m/s}^2]}\] よって運動方程式\(ma=F\)より \[\large{5.0\times 3.0=\underline{15.0\text{[N]}}}\] （２）\(t=4.0\)からの2.0[s]間の加速度は、 \[\large{a=\frac{6.0-6.0}{6.0-4.0}=0}\] より加速度は０、つまり加速度ははたらいていなかったと考えられます。 このとき、運動方程式より \[\large{5.0\times 0.0=0}\] となり、はたらいていた力は\(\large{\underline{0\text{[N]}}}\)となる。
（３）このときの加速度は \[\large{a=\frac{0.0-6.0}{8.0-6.0}=\underline{-3.0[\text{m/s}^2]}}\] またそのときにはたらく力は運動方程式より \[\large{5.0\times (-3.0)=\underline{-15.0[\text{N]}}}\] 加速度および力が負なので、速度の向きと逆向きとなります。つまり物体の速度が減少しているということになります。