力と運動(2)

運動というものは様々な物体に対してはたらくもので、以下のような２つの物体、AとBが糸でつながれた状態を考えます。右側にそれらを力\(F\)で引っ張っていくときの加速度を求めてみます。なお、２つの物体と床との摩擦は考えないものとし、糸には質量がないものとします。

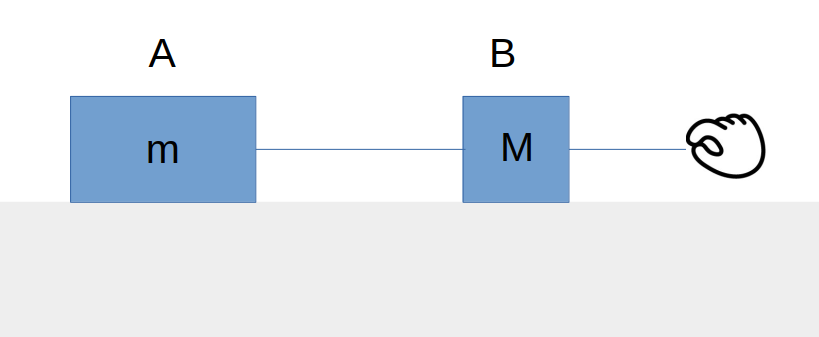
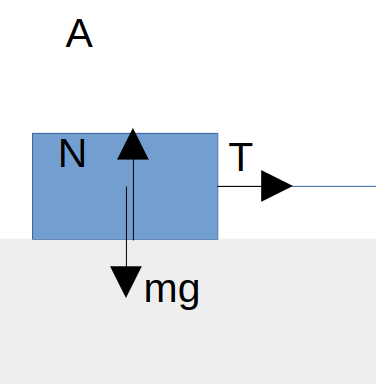
物体Aの質量を\(m\)、物体Bの質量を\(M\)とします。まず、物体Aに着目して力を描き入れます。

物体Bについても同様に考えます。鉛直下向きに重力\(Mg\)、垂直抗力が上向きに\(N'\)がはたらきます。これらは右向きには関係ありません。

物体Bに接触している部分は左側と右側の糸がつながっている部分です。左側には物体Aにはたらく張力の反作用として、物体Bの左向きに張力Tがはたらきます（作用反作用の法則によりこの２つの張力Tの大きさは等しいです）。

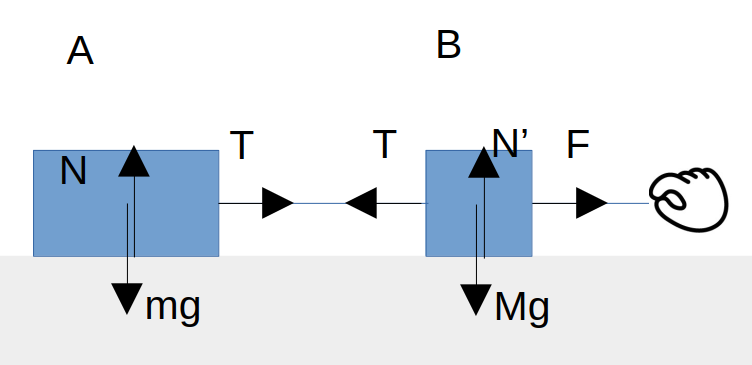
一方、物体Bの右向きには引っ張る力として\(F\)がはたらきます。これらから運動方程式をそれぞれの物体について立てていきます。

物体Aの運動方程式は、右向きを正として

\[\large{ma=T}\]

です。物体Bは、

\[\large{Ma=F-T}\]

となります。両方の式を連立して、

\[\large{\begin{align} ma &=T \\ Ma &=F-T\end{align}}\]]

\(T\)を消去して（作用反作用の法則により\(T\)の大きさは等しい）、

\[\large{\begin{align} ma &= F-Ma \\ (m+M)a &= F \\ a &= \frac{F}{m+M}\end{align}}\]

とわかります。