力と運動(3)
問1.右図のように、質量が\(m\)の物体Aと質量が\(M\)の物体Bが質量の無視できる軽い糸でつながれている。これらを上方に一定の力\(F\)で持ち上げるとき、生じる加速度\(a\)を求めよ。また、そのときの物体Bにかかる張力\(T\)を求めよ。ただし、重力加速度は\(g\)とする。
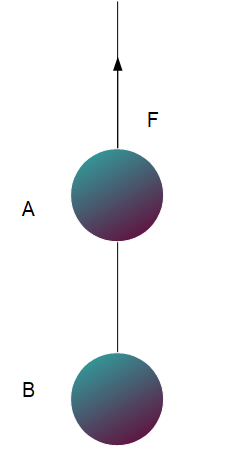
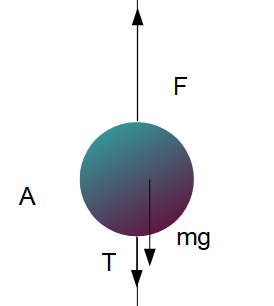
まず、物体Aに着目して、これにはたらく力を描き入れますと以下のようになります。
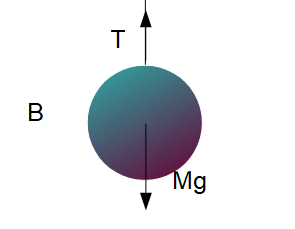
次に物体Bに着目して、はたらく力を描き入れます。
ここから、それぞれの物体について運動方程式を立てます。上向きを正とします。
\[\large{\begin{align}
ma &= F-(mg+T) & \cdots\text{物体A} \\
Ma &= T-Mg & \cdots\text{物体B}\end{align}}\]
物体Bの式から、
\[\large{T=M(a+g)}\]
これを物体Aの式に代入し、
\[\large{\begin{align}
ma &= F-mg-Ma-Mg \\
(m+M)a &= F-g(m+M) \\
a &= \underline{\frac{F}{m+M}-g}\end{align}}\]
この加速度\(a\)を物体Bの式に代入すると
\[\large{\begin{align}
M\left(\frac{F}{m+M}-g\right) &= T-Mg \\
T &= \underline{\frac{M}{m+M}F}\end{align}}\]
