力と運動(4)

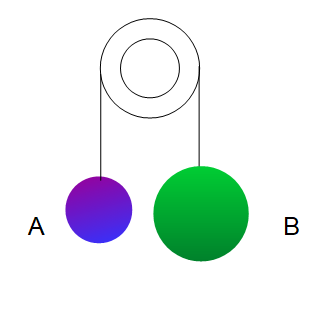
例によって、物体Aおよび物体Bにはたらく力を図示していきます。

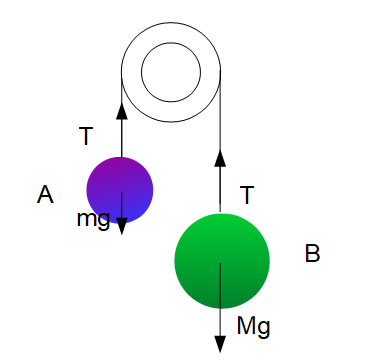
それぞれには重力および、糸からの張力がかかります。張力\(T\)は作用・反作用の法則により物体A・Bに同じ大きさがはたらきます。
ここから物体AとBに対して運動方程式を立てます。それにはまず、それぞれの物体に対して座標を設定してあげる必要があります。
問題文より\(m < M\)とあることから手を離すと物体Aは上へ、物体Bは下に運動するはずです。そのため、物体Aは上向きを正、物体Bは下向きを正とします。

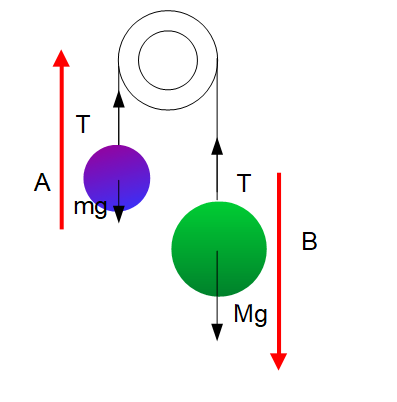
よって、それぞれの運動方程式は以下のようになります。 \[\large{\begin{align} ma=T-mg & \qquad\cdots\text{物体A} \\ Ma=Mg-T & \qquad\cdots\text{物体B}\end{align}}\] 両式を足して\(T\)を消去すると、 \[\large{(m+M)a=(M-m)g}\] より、 \[\large{\underline{a=\frac{M-m}{M+m}g}}\] また、これを代入して、 \[\large{\begin{align} \frac{M-m}{M+m}mg &= T-mg \\ T &= \frac{M-m}{M+m}mg+mg \\ &= \frac{M-m}{M+m}mg+\frac{M+m}{M+m}mg \\ &= \frac{Mmg+Mmg}{M+m} \\ &= \underline{\frac{2Mm}{M+m}g}\end{align}}\]