動摩擦力(2)
今、質量\(m\)の物体をあらい面において力Fを加えて左方向に初速度を与えたときの加速度を求めてみましょう。図示すると右のようになります。
物体にかかる力として、重力\(mg\)、垂直抗力\(N\)、押す力\(F\)と物体が動くので動摩擦力\(f\)がはたらいています。
物体の運動方向は面に水平方向左向きなので垂直方向の力はつり合っており、
\[\large{N=mg}\]
となります。
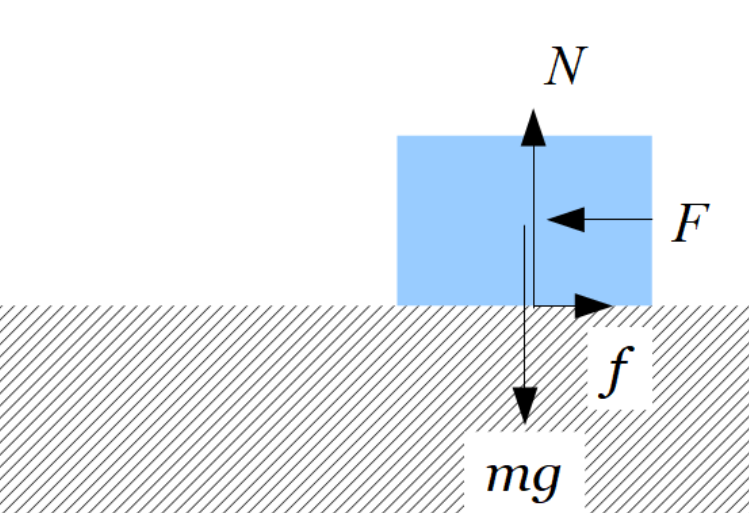
物体にはたらく力を図示したところで、動摩擦力\(f\)は
\[\large{f=\mu'N}\]
となるから、\(N=mg\)より
\[\large{f=\mu' mg}\]
よって、物体が左向きにはたらいている力は、
\[\large{F-\mu' mg}\]
です。運動方程式を立てると
\[\large{\begin{align}ma &= F-\mu' mg \\ a&=\frac{F}{m}-\mu'g\end{align}}\]
となります。力\(F\)を考慮せずに初速度を与えたとする場合、加速度は
\[\large{a=-\mu'g}\]
で与えられます。
