動摩擦力(3)

問題文と、そこから読み取れる物体にはたらく力を図示すると以下のようになります。

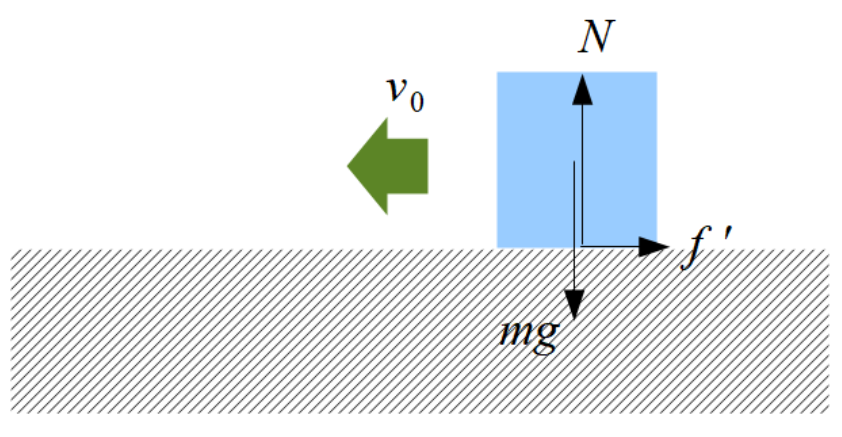
ここから、加速度\(a\)は動摩擦力\(f'=\mu'N\)を踏まえて \[\large{ma=-\mu'mg \\ \therefore a=-\mu'g}\] また、\(v=v_0+at\)より、物体が静止することから\(v=0\)として \[\large{\begin{align}v_0-\mu'gt &=0 \\ -\mu'gt &=-v_0 \\ t &= \underline{\frac{v_0}{\mu'g}}\end{align}}\] そのときに進んだ距離は\(x=v_0t+\dfrac{1}{2}at^2\)より \[\large{\begin{align}x &=\frac{v_0}{\mu'g}v_0-\frac{1}{2}\mu'g\left(\frac{v_0}{\mu'g}\right)^2 \\ &=\frac{v_0^2}{\mu'g}-\frac{v_0^2\mu'g}{2(\mu'g)^2} \\ &=\frac{v_0^2}{\mu'g}-\frac{v_0^2}{2\mu'g} \\ &=\frac{2v_0^2}{2\mu'g}-\frac{v_0^2}{2\mu'g} \\ &=\underline{\frac{v_0^2}{2\mu'g}}\end{align} }\]