速さと速度(5)
物体の運動で最も単純なものは等速直線運動です。等速直線運動とは物体が直線上を一定の速度で一方向に運動することを表します。つまり、その運動中は速度の変化はしないし、物体が曲がったり回転したりもしません。このとき、物体がある一定時間で動いた変位は速度に比例します。
これは算数で学んだものと全く同じことを言っているにすぎません。要するに距離=速さ×時間という式を、厳密に言葉を定義しなおしているだけです。では変位や速度を用いて式を立て直すと、変位を\(x\)、速度を\(v\)、時間を\(t\)とすれば
\[\large{x=vt}\tag{1}\]
となります。ここで、<b>等速</b>直線運動ですから、速度\(v\)は変わりません。よって(1)式は時間\(t\)のみで変化する一次関数だということが言えます。それが、変位が速度に比例するといっている意味に他なりません。
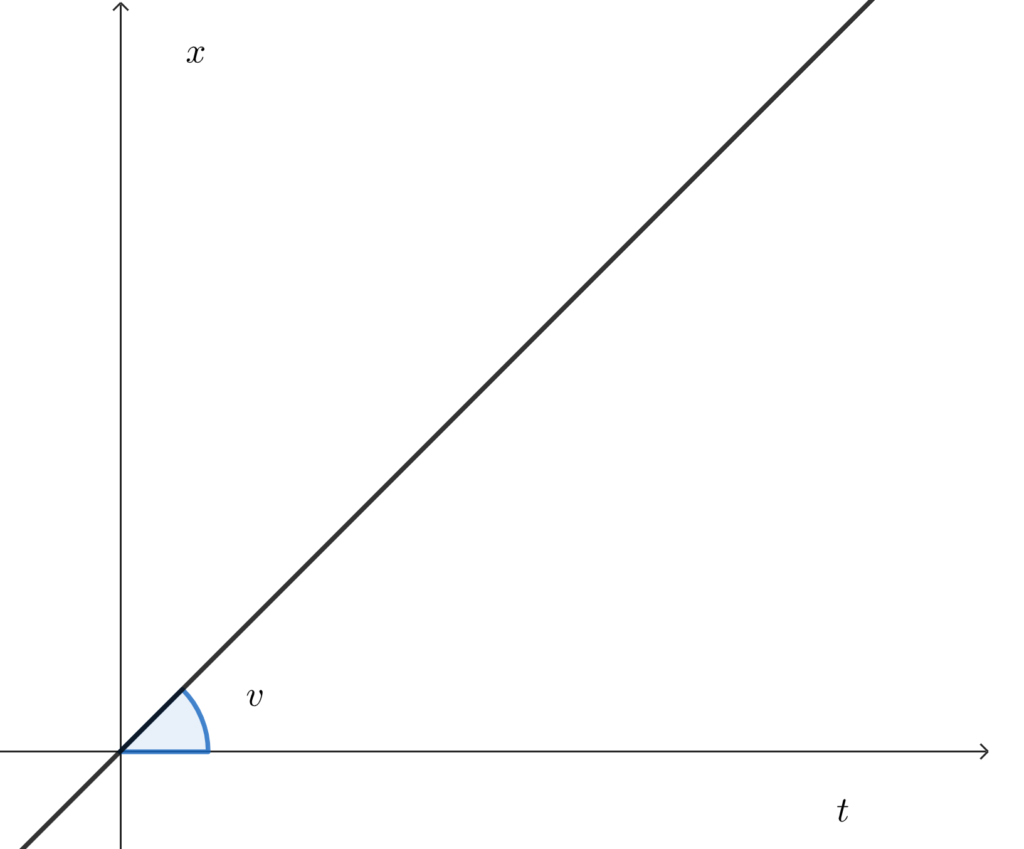
では、ここで等速直線運動のグラフを描いてみましょう。今、等速直線運動をする物体が時刻\(t=0\)秒の時に位置0にいたとき、縦軸に変位\(x\)、横軸に時間\(t\)をとったグラフは右のようになります。
グラフを見ればわかる通り、明らかに正比例のグラフです。この直線の傾きは速度\(v\)を表します。
このグラフを\(x-t\)グラフと呼んでいます。
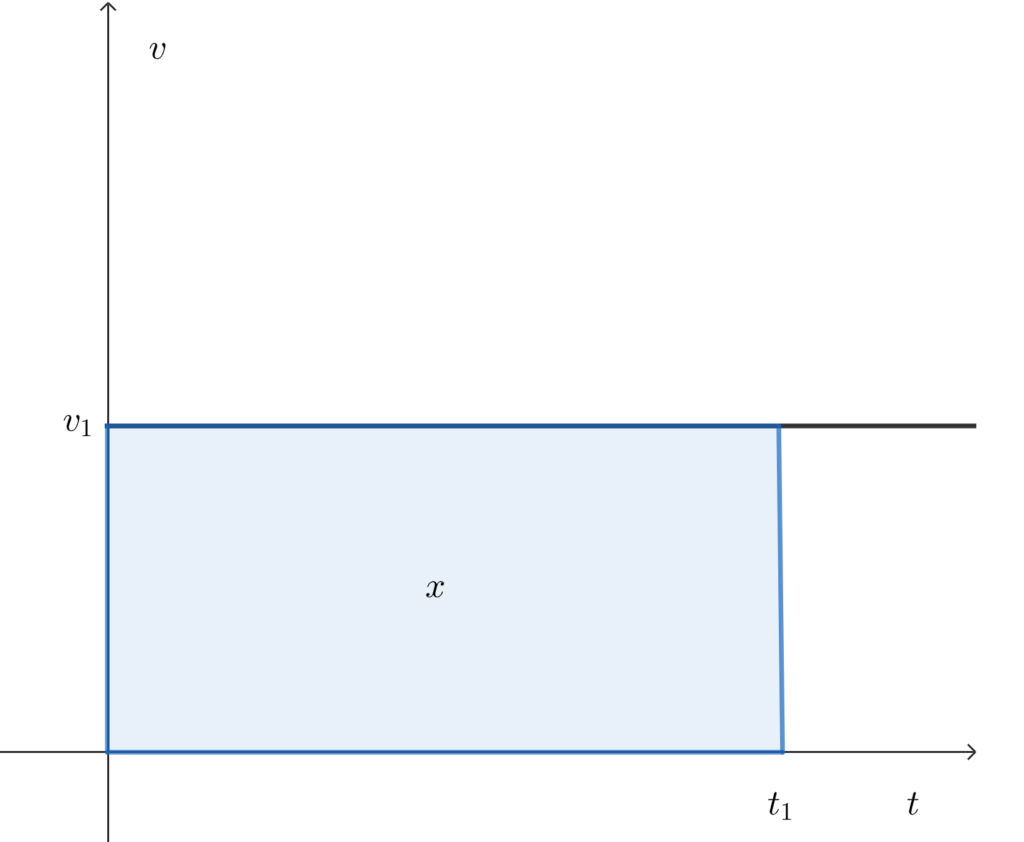
一方、縦軸に速度\(v\)、横軸に時間\(t\)をとって、同様の等速直線運動をグラフにしましょう。すると、速度\(v\)は一定の値をとり続けるため\(t\)軸に平行な直線となります。
等速直線運動の速度が\(v_1\)で時刻0から\(t_1\)まで経過したとき、\(v_1\)と\(t_1\)で囲まれた面積は変位\(x\)を意味します。これは変位の定義そのものです。
右図のように縦軸に速度\(v\)、横軸に時間\(t\)をとったグラフを\(v-t\)グラフと呼んでいます。
※\(v-t\)グラフで面積を求めること(=変位を求めること)は積分の定義そのものです。関数\(v=v_1\)を時間\(t\)で積分すれば変位が求められます。数式では時刻\(t=0\)から\(t=t_1\)までの積分となり
\[x=\int^{t_1}_{0} v_1 dt\]
で表されます。
