空気抵抗と終端速度(1)
通常、われわれが見る落下運動は空気中での出来事なので空気抵抗を受けながら落下します。なお、空気がない真空状態ではどのような物体でも落下速度は変わりません。
質量が同じ物体でも、空気抵抗を受けにくい球体と、薄く引き延ばした板状の物体では球体の方が早く落下し、板状の物体は空気抵抗をより受けるため遅く落下します。
物体にはたらく空気の抵抗力は、落下の速度を小さくすることから落下(運動)の向きとは逆向きにはたらきます。
抵抗力の大きさを\(f\)[N]とすると、物体の速さが空気に対してあまり大きくないときは物体の速さに比例することがわかっています。比例定数を\(k\)とおくと、空気の抵抗力は物体の速さを\(v\)[m/s]とすれば
\[\large{f=kv}\]
で表されます。
では具体的に、質量\(m\)の物体が空気中を落下するときに、空気抵抗によってどのようになるかを考えてみます。
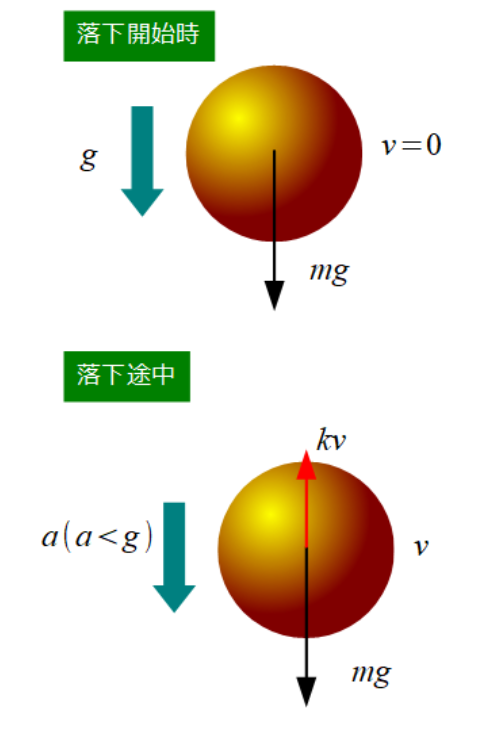
物体が落下し始めようとするときは、物体の速さは0なので、空気抵抗はかからない。よって、物体の加速度は重力加速度\(g\)に等しいです。
物体は落下するにつれて速さは増していきます。速さが増せば空気の抵抗力も大きくなっていきます。ある一時点の物体の速さを\(v\)とすると、空気の抵抗力は鉛直上向きにはたらくので、物体の加速度を\(a\)として鉛直下向きを正とするときの運動方程式は
\[\large{ma=mg-kv \\ a=g-\dfrac{kv}{m}\qquad (0 < a < g)}\]
上記式より、\(v\)が小さいときには\(a > 0\)ということから物体の速さはだんだん大きくなっていきます。一方、\(v\)が大きくなっていくと、\(a\)は0に近づきますので、速さは徐々に小さくなっていきます。
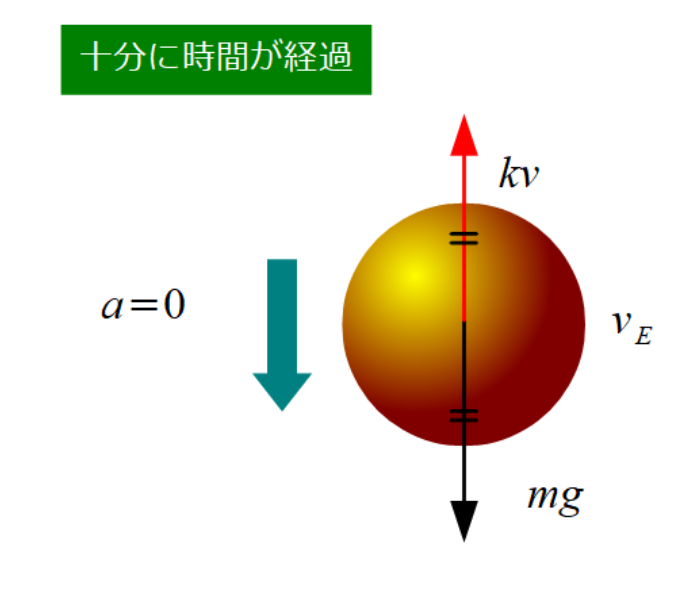
十分に時間が経過して、物体の速さが大きくなり空気の抵抗力と重力がつりあうと\(a=0\)となって、物体は一定の速さで落下していきます。この一定の速度を終端速度といいます。
終端速度を\(v_E\)とすると、物体にはたらく力のつり合いから
\[\large{mg-kv_E=0 \\ v_E=\frac{mg}{k}}\]
となります。物体の形や大きさが等しく、\(k\)も同様に等しければ終端速度は質量\(m\)が大きければ終端速度も速くなります。