力のモーメント(2)
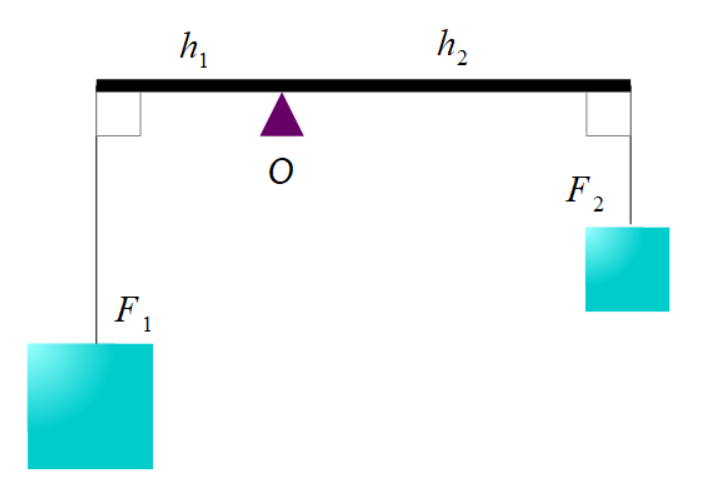
右図のように、1点\(O\)で支えられた軽い棒の両端に質量\(F_1,F_2\)の物体を軽い糸で吊るすとき、
\[\large{h_1F_1=h_2F_2}\]
が成り立つならば棒は平行状態でつり合います。
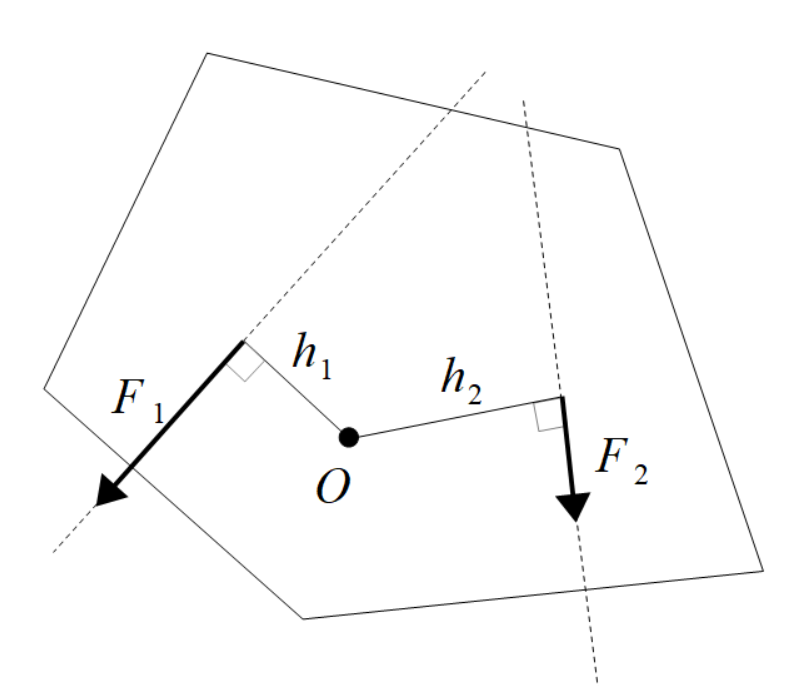
また、点Oを回転軸として回転するようにした物体に、任意の作用線上に力\(F_1,F_2\)を加えるとき、点Oから力の作用点までの距離\(h_1,h_2\)との間に同じように
\[\large{h_1F_1=h_2F_2}\]
が成り立つならば、物体は回転せずにその場にとどまります。
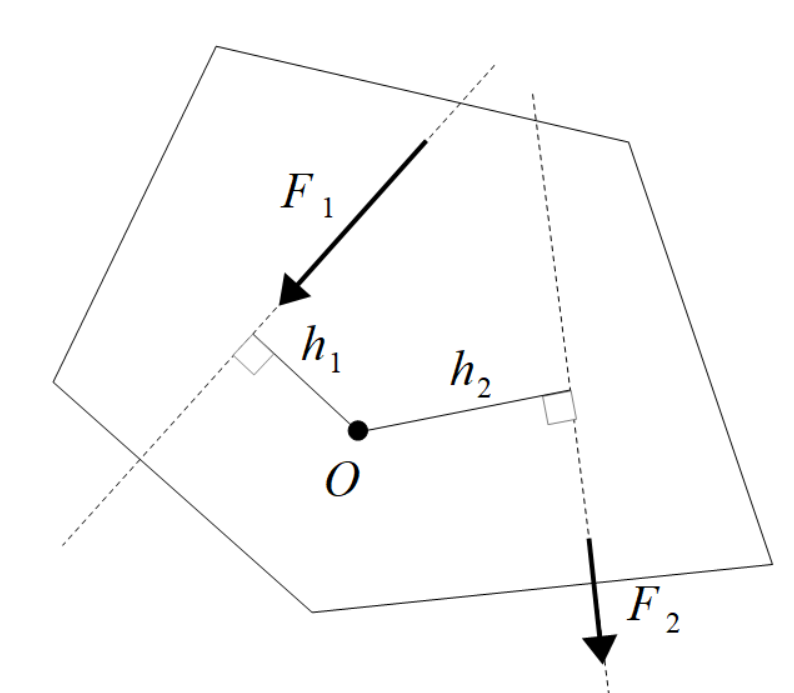
力の作用線上にはたらく力は作用点が異なっても物体に与える効果は等しくなります。したがって、右図のような力の加え方でもこの物体は回転せず、その場にとどまり続けます。
つまり、\(h_1,h_2\)は点Oから作用線までの距離だけを考えればよいということになります。
以上のことから、ある点Oのまわりに物体を回転させる力は、力の大きさ\(F\)と、点Oから作用線までの距離\(h\)の積\(Fh\)で表されることとなり、これを力のモーメントと呼んでいます。ちなみに点Oから作用線までの距離をうでの長さと呼んでいます。力のモーメントの単位はその定義から、N・mです。
