力のモーメント(4)
問1.以下のように長さ1の棒ABがあって、中点Oを回転軸としてAから\(\dfrac{3}{4}\)の点に45°の角度で力\(F\)を加える。このとき、以下の点における力のモーメントを求めよ。ただし反時計回りを正とする。
(1)点A (2)点O (3)点B
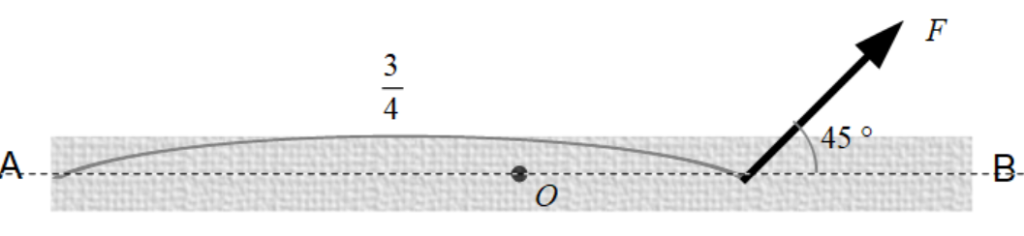
(1)力Fを水平方向と垂直方向に分解すると以下のようになります。
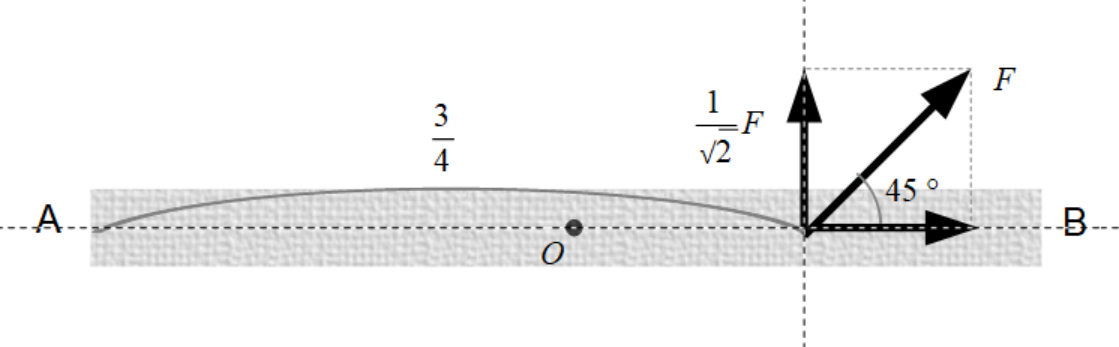
点Aは力のモーメントの公式により、
\[\large{M=\dfrac{3}{4}\cdot\dfrac{1}{\sqrt{2}}F=\underline{\dfrac{3}{4\sqrt{2}}F}}\]
(2)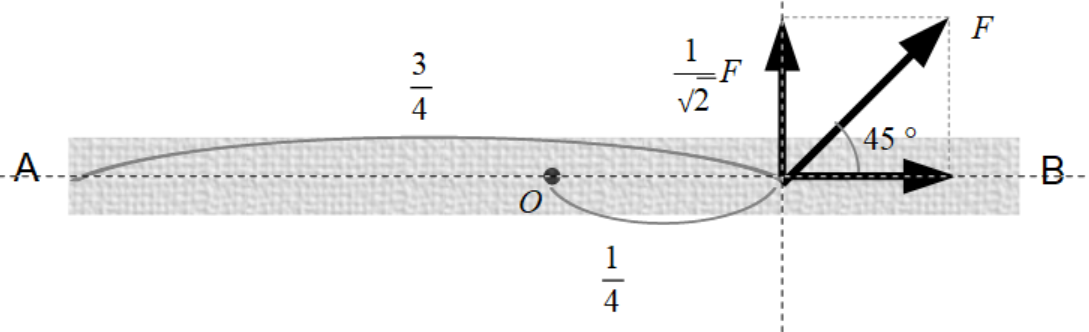
点Oにおけるうでの長さは\(\dfrac{3}{4}-\dfrac{1}{2}=\dfrac{1}{4}\)。よって、
\[\large{M=\dfrac{1}{4}\cdot\dfrac{1}{\sqrt{2}}F=\underline{\dfrac{1}{4\sqrt{2}}F}}\]
(3)点Bは力の作用点より右側にあるので時計回り。したがって、力のモーメントは負になります。
\[\large{M=-\dfrac{1}{4}\cdot\dfrac{1}{\sqrt{2}}F=\underline{-\dfrac{1}{4\sqrt{2}}F}}\]
